Сигналов

Спектр непериодических (одиночных импульсных)

Для исследования непериодических сигналов воспользуемся ранее рассмотренным методом спектрального анализа периодических сигналов, устремив к бесконечности период повторения (17.1) и (17.2). При этом окажется:

-во-первых, частоты соседних гармоник nω₁ и (n + 1) ω₁ станут сколь угодно близки друг к другу и потому дискретную переменную nω₁ можно заменить непрерывной переменной ω – текущей частотой;

-во-вторых, амплитудные коэффициенты ряда Фурье а₀, а_n и b_n станут неограниченно малыми из-за наличия величины Т в формулах (17.4).

В таких условиях спектральный анализ периодического сигнала по расположению его гармоник Фурье вдоль дискретной оси частот представляют в виде спектральной плотности непериодического сигнала вдоль непрерывной оси частот. Математическим аппаратом спектрального анализа непериодических сигналов служит так называемое преобразование Фурье:

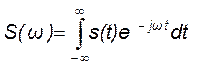. (17.6)

Из выражения (17.6) следует, что спектральная плотность - комплексозначная функция частоты, одновременно несущая информацию как об амплитуде, так и фазе гармонических составляющих Фурье.

Зная спектральную плотность непериодического сигнала, можно найти математическое выражение самого сигнала, воспользовавшись математическим аппаратом обратного преобразования Фурье:

. (17.7)

Формулы (17.6) и (17.7) допускают одновременное существование двух математических моделей одного и того же сигнала в частотной и временной области при условии, что исследуемый сигнал является абсолютно интегрируем, т.е. существует интеграл

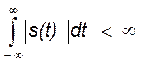. (17.8)

Условие (17.8) сужает вид допустимых сигналов для исследования их спектральной плотности, например, невозможно говорить о спектральной плотности гармонического сигнала, из-за того, что он существует на всей бесконечной оси времени.

В качестве примера рассмотрим спектральную плотность одиночного прямоугольного видеоимпульса с длительностью τ_И и амплитудой А₀.

На основании формулы (17.6) получим:

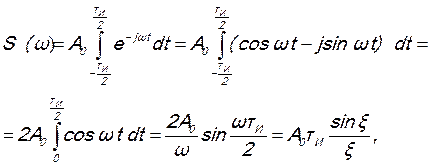(17.9)

где 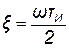- безразмерная переменная.

График, построенный по формуле (17.9) и пронормированный значением спектральной плотности S(0), изображен на рис. 17.3

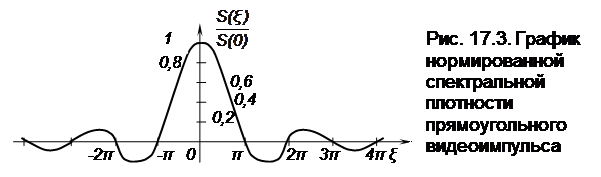Значение спектральной плотности при ξ = 0 соответствует площади прямоугольного видеоимпульса:

.

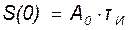Другим примером нахождения спектральной плотности непериодического сигнала является экспоненциальный видеоимпульс

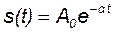, (17.10)

который, строго говоря, не является импульсом, так как его амплитуда принимает нулевое значение (рис. 17.4) при t → ∞.

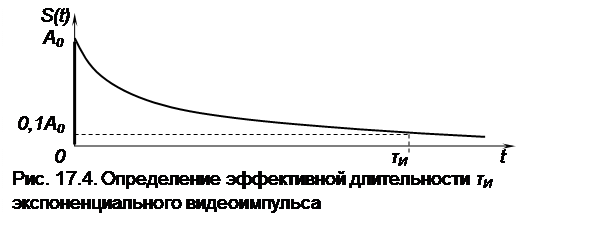Однако формулу (17.10) можно представить к виду с конечным значением аргумента, например, как это проиллюстрировано на рис. 17.4.

Спектральная плотность экспоненциального видеоимпульса принимает значение

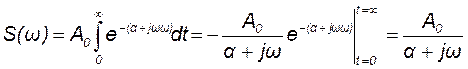, (17.11)

Из выражения (17.11) находим модуль (амплитудный спектр) и аргумент (фазовый спектр) спектральной плотности экспоненциального видеоимпульса соответственно:

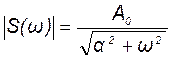, (17.12)

(17.13)

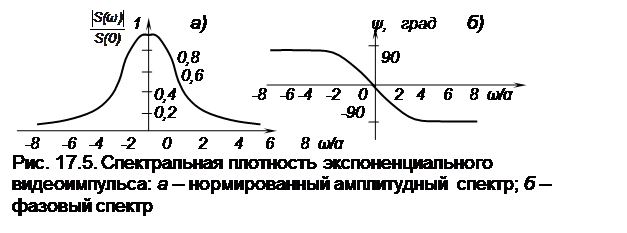
Графики нормированного амплитудного (17.12) и фазового (17.13) спектров экспоненциального видеоимпульса представлены на рис. 17.5.

Определим спектральную плотность δ – импульса (дельта функции).

Математическая модель дельта – импульса представлена выражением:

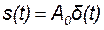. (17.14)

Спектральная плотность сигнала (17.14) имеет вид

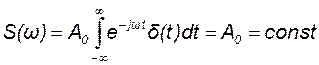. (17.15)

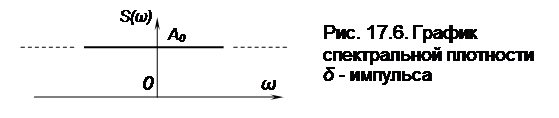
Из анализа математического выражения (17.15) следует, что дельта – импульс имеет равномерный спектр на всех частотах, что проиллюстрировано на рис. 17.6.

В момент возникновения дельта- импульса все элементарные гармонические составляющие складываются когерентно.

Таким образом, были рассмотрены спектральные представления электромагнитных сигналов, основанные на использовании теории разложения исследуемых как периодических, так и непериодических сигналов в ряд Фурье.

Тест 39

Дата добавления: 2014-01-15