Основные характеристики случайных величин

Лекция 18. Случайные электромагнитные сигналы

Тема 5. Электромагнитные сигналы и их преобразование

В условиях, когда мгновенные значения сигнала заранее не предсказуемы и детерминированное его описание принципиально невозможно, применяют вероятностные (статистические) модели этого сигнала.

Основные характеристики случайных величин представляются следующими понятиями и определениями [5]:

Вероятностью наступления случайного события. Каждому событию 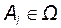сопоставляется вещественное число 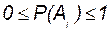, которое называется вероятностью этого события, где Ω = {A₁, A₂, …,A_n }.

Сумма всех событий, содержащих в Ω, есть достоверное событие:

Р(А₁)+Р(А₂)+…+Р(А_п) = 1.

Вероятность случайных событий оценивают относительной частотой благоприятных исходов:

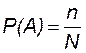, (18.1)

где N - число независимых друг от друга испытаний (опытов).

Случайной величиной Х называется совокупность всевозможных вещественных чисел х, принимающих случайные значения.

Если случайная величина Х может принимать любые значения, то неслучайная функция 0 ≤ F(x)≤ 1 вещественного аргумента х является неубывающей функцией распределения этой случайной величины, предельные значения которой удовлетворяют условию:

F (- ∞) = 0 и F (∞) = 1.

Функция распределения F(x) случайной величины Х определяется как распределение вероятности того, что случайное число из Х примет значение, не превышающее конкретного х:

F(x) = P(X ≤ x).

Производная от функции распределения

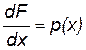
есть плотность распределения вероятности (или, короче, плотность вероятности) данной случайной величины Х.

Для непрерывной случайной величины Х плотность вероятности р(х) представляет собой гладкую функцию. Если же Х – дискретная случайная величина, принимающая фиксированные значения {x₁, x₂, …, x_n, …} c вероятностью {P₁, P₂, …, P_n, …} соответственно, то для нее плотность вероятности выражается как сумма дельта – функций:

.

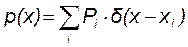В обоих случаях плотность вероятности должна быть неотрицательной р(х) ≥ 0 и удовлетворять условию нормировки

.

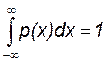В теории случайных сигналов фундаментальное значение имеет гауссова (нормальная) плотность вероятности

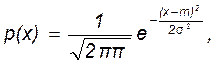(18.2)

где 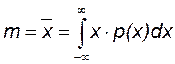─ (18.3)

─ математическое ожидание или среднее значение случайной величины;

─

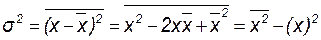─ дисперсия случайной величины, которая служит для количественного описания меры разброса результатов отдельных случайных испытаний относительно математического ожидания.

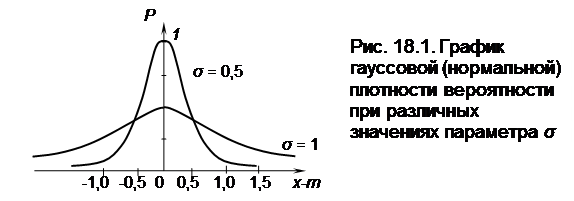
График гауссовой (нормальной) плотности вероятности при различных значениях параметра σ представлен на рис. 18.1.

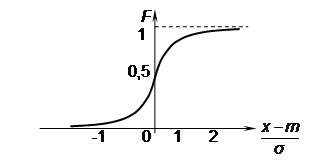
Функция распределения гауссовой случайной величины

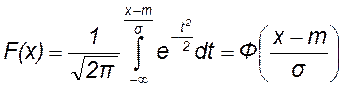, (18.4)

где 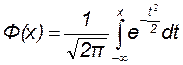─ интеграл вероятностей.

График функции распределения гауссовой (нормальной) случайной величины представлен на рис. 18.2.

		Рис. 18.2. График функции распределения гауссовой (нормальной) случайной величины

Современная радиотехника все шире применяет цифровые измерители параметров случайных сигналов как случайных процессов. Работа цифровых измерителей основана на дискретизации случайного сигнала и последующих операциях над числами-выборками.

Дата добавления: 2014-01-15