Сигнал как стационарный случайный процесс

Случайный процесс Х(t) – это особого вида функция, характеризующаяся тем, что в любой момент времени t,принимаемые ею значения, являются случайными величинами.

Случайный процесс представляет собой бесконечную совокупность фиксированных мгновенных значений, образующих статистический ансамбль реализаций, который характеризуется многомерной плотностью вероятности этого случайного процесса.

Случайный процесс является стационарным, если его функция корреляции R(τ) обладает свойством четности

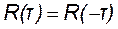
и, кроме того, абсолютные значения корреляционной функции при любых τ не превышают ее значения при τ = 0:

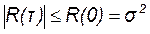. (18.5)

Корреляционная функция служит количественной мерой степени статистической связи тех случайных величин, которые наблюдаются в соседних между собой моментах времени t₁ и t₂, разделенных интервалом τ:

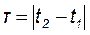. (18.6)

С помощью выражения (18.6) можно функцию корреляции записать как

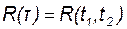. (18.7)

В стационарном случайном процессе математическое ожидание т и дисперсия σ² не зависят от времени

σ² = const; m = const. (18.8)

Пример 1. Модель случайного сигнала 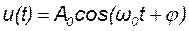, где ω₀ и А₀ заранее известны, характеризуется случайным равномерным изменением фазы на отрезке – π ≤ φ ≤ π. Определим условия стационарности случайного сигнала.

Плотность вероятности фазового угла .

Математическое ожидание получим:

.

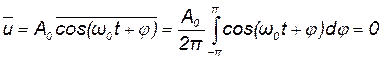Найдем дисперсию

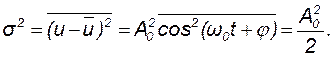
Наконец, получим искомую функцию корреляции:

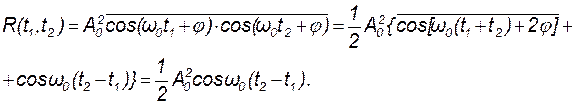
Итак, корреляционная функция четная, дисперсия и математическое ожидание не зависят от времени и потому исследуемый случайный сигнал является стационарным.

Пример 2. Амплитудно-манипулированный сигнал имеет четную корреляционную функцию

,

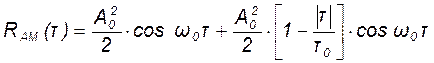где τ₀ – длительность элементарного символа двоичного кода «1» и «0»;

Большинство случайных процессов в радиотехнике являются эргодическими [4, 5].

Стационарный случайный сигнал является эргодическим, если усреднение его статистического ансамбля реализаций можно заменить усреднением по времени одной его единственной реализации.

Математическим достаточным условием эргодичности случайного сигнала является стремление к нулю функции корреляции при неограниченном росте временного сдвига (18.6):

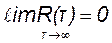. (18.9)

Одной из важнейших характеристик стационарного случайного сигнала является спектральная плотность его мощности (спектр мощности), которая определяется с помощью преобразований Фурье:

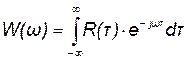. (18.10)

Спектральная плотность мощности стационарного случайного процесса, будучи всегда вещественной, не содержит никакой информации о фазовых соотношениях между отдельными спектральными составляющими. По спектру мощности невозможно восстановить отдельно взятую реализацию случайного процесса.

Так как корреляционная функция стационарного случайного сигнала четная, то для количественной оценки эффективной ширины его частотного спектра используют экстремальное (максимальное) значение одностороннего F(ω) спектра мощности

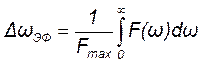. (18.11)

Если на всех частотах спектральная плотность мощности является постоянной величиной, то такой стационарный случайный процесс называется «белым шумом»

W(ω) = W₀ = const. (18.12)

Для белого шума

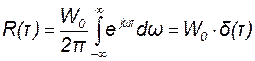. (18.13)

Средняя мощность N₀ (дисперсия) белого шума неограниченно велика.

Реальные, достаточно широкополосные, стационарные случайные процессы в электротехнике заменяют белым шумом.

Таким образом, были приведены основные характеристики случайных величин (вероятность, математическое ожидание, дисперсия) и рассмотрен электромагнитный сигнал как стационарный случайный процесс.

Тест 41

Дата добавления: 2014-01-15