Основные теоремы и положения алгебры логики

Принцип двойственности.

Запишем алгоритм выполнения операций ИЛИ и И, расположив строки таблицы для операции И в обратном порядке – снизу вверх:

ИЛИ	0 Ú 0 = 0	И	1 · 1 = 1
0 Ú 1 = 1	1 · 0 = 0
1 Ú 0 = 1	0 · 1 = 0
1 Ú 1 = 1	0 · 0 = 0

Если в этих таблицах переменные заменить их инверсиями, а знаки дизъюнкции на знаки конъюнкции и наоборот, то алгоритмы меняются местами. Таблица истинности для ИЛИ становится таблицей истинности для И и наоборот.

В этом состоит принцип двойственности, который в общем виде записывается так:

, .

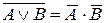Для любого числа переменных это правило, называемое еще теоремой де Моргана, имеет вид:

; .

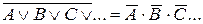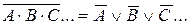На практике принцип двойственности приводит к тому, что логи-ческий элемент, выполняющий в положительной логике операцию И, в случае отрицательной логики будет выполнять операцию ИЛИ.
Для преобразования выражений алгебры логики с целью их упрощения или приведения к удобному виду используются, как и в обычной алгебре, скобки, а если их нет, то сначала выполняется отрицание (инверсия) над отдельными переменными, затем логическое умножение (конъюнкция), затем логическое сложение (дизъюнкция). Если же знак инверсии расположен над целым выражением, то она выполняется в последнюю очередь. В процессе преобразования формул используются теоремы алгебры логики.

Теоремы для одной переменной:

1. A Ú 0 = A. 4. A Ú Ā = 1. 7. A · A = A.

2. A Ú 1 = 1. 5. A · 0 = 0. 8. A · Ā = 0.

3. A Ú A = A. 6. A · 1 = 1. 9. .

Эти теоремы легко проверяются подстановкой A = 1, A = 0 и остаются справедливыми (как и последующие) для случаев, когда под A понимают не только одно переменное, но и целое выражение.

Теоремы для двух и более переменных:

10. а) A Ú B = B Ú A, б) AB = BA – переместительный закон,

означает, что все входы логического элемента равнозначны.

11. а) A Ú B Ú C = A Ú (B Ú C) = (A Ú B) Ú C,

б) ABC = A (BC) = (AB) C – сочетательный закон.

12. а) A (B Ú C) = AB Ú AC, б) A Ú BC = (A Ú B)(A Ú C) – распределительный закон.

Данная теорема и все последующие вытекают из принципа двойственности. Применим его к выражению 12, а:

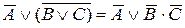– левая часть,

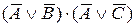– правая часть.

Введя новые обозначения: 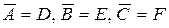, получим: 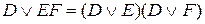, а это и есть теорема 12, б.

13. а) A Ú AB = A, б) A (A Ú B) = A – закон поглощения (A погло-

щает B).

Доказательство 13, а:

A Ú AB = A (1 Ú B) = A · 1 = A, (используя теоремы 2, 6).

Теорема 13, б следует из принципа двойственности.

14. а) 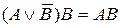, б) .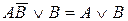

Доказательство 14, а:

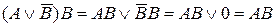, (используя теоремы 8 и 1).

Теорема 14, б следует из принципа двойственности.

15. а) AB Ú ĀB = B, б) (A Ú B)(Ā Ú B) = B, закон склеивания (склеивание по A).

Доказательство 15, а:

AB Ú. ĀB = B (A Ú Ā) = B · 1 = B, (используя теоремы 4 и 6).

Теорема 15, б следует из принципа двойственности.

Дата добавления: 2014-01-15