Логические (булевы) функции

Булева функция (F) является результатом выполнения логических операций над двоичными переменными – аргументами (A, B, C, …) и полностью зависит от их значений.

Задать булеву функцию – значит указать ее значения, (0 или 1) при всех возможных комбинациях значений переменных.

Каждая комбинация аргументов называется набором, при N аргументах существует 2 ^N наборов.

Если известны значения функции на всех наборах аргументов, она называется полностью определенной. Если же на некоторых наборах значение функции не известно, то она называется недоопределенной, а соответствующие наборы – запрещенными наборами. В процессе упрощения функции ее значения на запрещенных наборах можно задать по своему усмотрению (доопределить функцию).

Логические функции могут иметь различные формы представления: словесную, табличную, алгебраическую, графическую..

Рассмотрим два примера словесного задания булевой функции.

Полностью определенная функция F ₁ трех аргументов A, B, C принимает значение 1, если два любых аргумента (или все три) равны 1.
В других случаях функция равна нулю. Количество наборов переменных равно 2 ³ = 8.

Недоопределенная функция F ₂ трех аргументов A, B, C принимает значение 1, если два любых аргумента равны 1, и равна нулю в остальных случаях, кроме случаев однозначности всех трех аргументов.

Если пронумеровать наборы от 0 до 2³ – 1, эти словесно заданные функции можно представить в виде таблицы истинности (табл. 2.2).

Таблица 2.2

Номера наборов	A	B	C	F 1	F 2	F 3	F 4
					–
					–

Функция F ₂ не определена на 0 и 7 наборах, где все три аргумента однозначны, поэтому в таблице 2.2 против этих наборов проставлены прочерки.

Отдельный интерес представляют функции F ₃и F ₄.

Конституентой единицы (F ₃) называют функцию n аргументов, которая принимает значение, равное единице, только на одном наборе аргументов. На всех остальных наборах она равна нулю.

Конституентой нуля (F ₄) называют функцию n аргументов, которая принимает значение, равное нулю, только на одном наборе аргументов.

От табличного задания булевой функции можно перейти к ее алгебраическому представлению, причем в двух формах: совершенной дизъюнктивной нормальной форме и совершенной конъюнктивной нормальной форме.

Совершенной дизъюнктивной нормальной формой (Сов ДНФ) функции называют дизъюнкцию конституент единицы – минтермов, взятых на тех наборах, на которых единице равна сама функция.

Минтерм – конъюнкция всех переменных в наборе, которые берутся в прямом виде, если их значение равно единице, либо в инверсном виде, если их значение в наборе равно нулю.

Функция F ₁ в Сов ДНФ будет иметь вид:

.

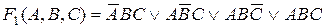Совершенной конъюнктивной нормальной формой (Сов КНФ) функции называют конъюнкцию конституент нуля – макстермов, взятых на тех наборах, на которых нулю равна сама функция.

Макстерм – дизъюнкция всех переменных в наборе, которые берутся в прямом виде, если их значение равно нулю, либо в инверсном виде, если их значение в наборе равно единице.

Функция F ₁ в Сов КНФ примет вид:

.

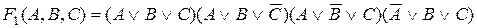Теоремы булевой алгебры позволяют достаточно просто перейти от одной формы представления булевой функции к другой. Однако, с точки зрения минимизации алгебраических выражений более удобна Сов ДНФ.

2.5. МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ

Аналитические методы минимизации

Используя законы булевой алгебры, можно получить для одной и той же логической функции множество эквивалентных представлений. Чем проще аналитическое выражение функции, тем экономичнее и проще ее практическая реализация на интегральных микросхемах. Сложность булевой функции определяется ее рангом, т.е. количеством переменных в ее конъюнктивных или дизъюнктивных членах.

Представление булевой функции в Сов ДНФ в большинстве случаев не является минимальным.

Используя операции поглощения и склеивания, его можно существенно упростить. Часто используется неполное склеивание, при котором оба члена, участвовавших в склеивании (или один из них), могут повторно склеиваться с другими оставшимися членами Сов ДНФ.

В процессе минимизации важно отыскать смежные конституенты, которые отличаются только одним аргументом (в одну конституенту аргумент входит с инверсией, а в другую – без нее).

Две смежные конституенты, склеиваясь, образуют импликанту рангом на единицу ниже, чем исходныеконституенты.

Используя, например, неполное склеивание последней коституенты в Сов ДНФ функции F ₁ последовательно с остальными, приходим к следующему выражению:

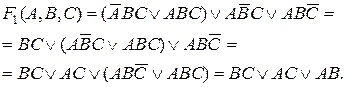
Процесс многоступенчатого склеивания приводит к импликантам, которые не склеиваются с другими. Такие импликанты называют простыми. Форма записи булевой функции в ДНФ, состоящая только

из простых импликант, называется сокращенной дизъюнктивной нормальной формой (Сокр ДНФ).

В некоторых случаях в Сокр ДНФ могут содержаться лишние импликанты, которые могут быть исключены без изменения значения функции.

Одним из методов отыскания лишних импликант является метод испытания членов: чтобы испытать некоторый член логической функции, следует исключить его из Сокр ДНФ и подставить в оставшееся выражение такие значения аргументов, которые обращают исключенный член в единицу. Если при такой подстановке оставшееся выражение окажется тождественно равным единице, то испытуемый член является лишним.

Найдем для примера тупиковую форму (без лишних импликант) Сокр ДНФ .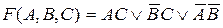

Испытаем член AC. AC = 1, если A = 1 и C = 1. Подставим в оставшееся выражение 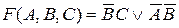A = 1 и C = 1, получим 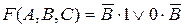. При B = 0 F (A, B, C) = 1·1 Ú 0·1 = 1, но при F (A, B, C) = 0·1 Ú 0·0 = 0. Следовательно, член AC не лишний.

Испытаем член BC, равный 1 при B = 0, C = 1. При этом 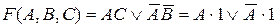. Последнее выражение равно 1 как при A = 1, так и при A = 0. Поэтому член 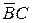– лишний.

Испытание члена по этой же методике показывает, что он не является лишним, в итоге тупиковая форма исходной функции имеет вид:

.

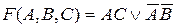Дата добавления: 2014-01-15