Кинематические характеристики плоской скалярной волны

В общем случае уравнение плоской скалярной волны можно записать в виде

S = f (t, x) (1.7)

Это уравнение означает, что скалярный параметр S в любой заданный момент времени имеет одно и то же значение во всех точках плоскости x = x ₁ = cons t.

Наибольший интерес для нас будет представлять волна, в которой координата (х) и время (t) входят в уравнение (1.7) в виде линейной комбинации

S = f (at - bx). (1.8)

Здесь a и b — постоянные,

f — функция, определяющая форму передаваемого сигнала.

Мы будем рассматривать распространение гармонического колебания, когда параметр S меняется во времени и в пространстве по гармоническому закону.

a) Осциллограмма волны: S = f (t).

Рассмотрим зависимость S = f (t) для двух плоскостей x = 0 и x = x ₁.

x = 0 S (t,0)= S (at) (1.9)

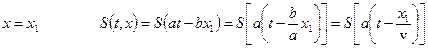(1.10)

Сравнение уравнений (1.9) и (1.10) показывает, что изменение параметра S в плоскости x, в точности повторяет изменение этой величины в плоскости x = 0, но с запаздыванием на 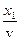, где .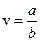

b) Фотография волны.

Рассмотрим фотографию волны в плоскости x в моменты времени t = 0 и t = t ₁.

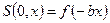(1.11)

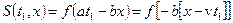. (1.12)

Сопоставляя эти уравнения, приходим к выводу, что волна не меняет своей формы: за время t ₁ сигнал перемещается со скоростью 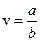вдоль оси Х на расстояние v t ₁. Волна при этом не деформируется.

Вывод:

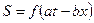— уравнение плоской скалярной, недеформируемой волны, распространяющейся со скоростью 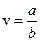в положительном направлении оси x.

В случае синусоидальной волны f — гармоническая функция координаты и времени.

Путь в плоскости, проходящей через начало координат, происходят колебания с частотой ω (рис. 1.2).

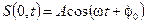
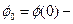начальная фаза колебаний.

В плоскости, отстоящей от исходной на расстоянии l, эти колебания повторяются с запаздыванием 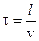.Здесь v — скорость распространения волны.

Колебания в точке, определяемой радиус – вектором 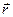(рис.1.2):

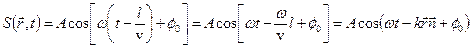
Мы пришли к уравнению плоской гармонической волны, распространяющейся в произвольном направлении.

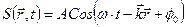(1.14)

Рис. 1.2

Здесь: 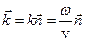— волновой вектор,

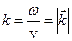— волновое число.

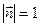— единичный вектор, совпадающий по направлению с направлением распространения волны.

Волновой вектор 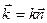— тоже указывает направление движения волны.

В частном случае

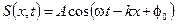(1.15)

Формула 1.15 — уравнение плоской волны, движущейся в положительном направлении оси Х.

Это монохроматическая (одноцветная) волна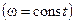

Зафиксировав какое – либо значение фазы волны, получим уравнение движения выбранной фазовой поверхности (в нашем случае – плоскости)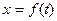

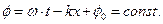(1.16)

Волновой (фазовой) поверхностью называется геометрическое место точек, в которых фаза волны имеет одинаковое значение.

Продифференцируем уравнение (1.16) по времени:

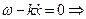
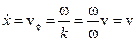. (1.17)

Скорость движения фазовой поверхности v_ф равна скорости распространения волны. Если плоская волна движется в отрицательном направлении оси x, то v < 0 и уравнение волны принимает вид

.

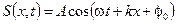Уравнение волны 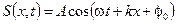является решением дифференциального волнового уравнения:

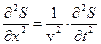. (1.18)

Докажем это, показав, что гармоническая функция (1.15) обращает дифференциальное уравнение (1.18) в тождество.

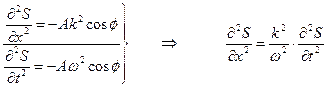
Здесь 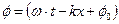— фаза волны.

.

Рассмотрим две фазовые поверхности плоской волны

.

.

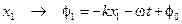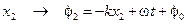Разность этих фаз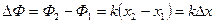

Колебания, происходящие со сдвигом по фазе, кратным 2π, называются

синфазными. Иными словами, разность фаз двух синфазных колебаний равна

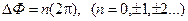
Минимальное расстояние между двумя фазовыми поверхностями, в которых происходят синфазные колебания, называется длиной волны (λ)

.

.

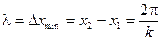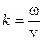Поэтому

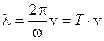. (1.19)

Здесь: 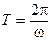— период колебания,

λ — длина волны. Длину волны теперь можно определить как расстояние, которое проходит волна за время одного полного колебания T (λ = v T).

Дата добавления: 2014-01-15