Частотный анализ систем автоматического управления

Предварительно рассмотрим комплексные числа и основные операции над ними. Существует три формы записи комплексного числа

1. Обычная форма W = W_x+ j W_y, j =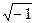- мнимая единица. (2.4.1)

2. Тригонометрическая форма W = A(cosy + j siny). (2.4.2)

3. Показательная форма W = A e^{jy .}. (2.4.3)

Комплексное число представляет собой точку на комплексной плоскости с действительной и мнимой частями W_x, W_y. Точке соответствует вектор с длиной (модулем) А и аргументом (фазой) y (рис. 2.4.1). На рис.2.4.1 на осях последо­вательно перечислены встречающиеся в сочетании типовые обозначения веще­ственной и мнимой осей.

Положительное направление отсчета углов – против часовой стрелки. Из (2.4.1) – (2.4.3) и рис. 2.4.1 вытекают соотношения:

W_x = Acosy; 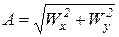; W_y = Asiny; . (2.4.4)

Пусть W₁ = A₁e^jy1 и W₂ = A₂e^jy2.

Тогда 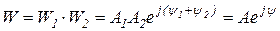_; (2.4.5)

, (2.4.6)

т. е. при перемножении комплексных чисел их модули перемножаются, а аргу­менты складываются. В случае деления комплексных чисел их модули делятся, а аргументы вычитаются.

Заметим также, что произведение комплексно-сопряженных чисел дает квадрат модуля, т.е. W×W^*=(W_x + j W_y ) (W_x – j W_y )=W_x ² + W_y ² = A ². (2.4.7)

Если имеем дробь , (2.4.8)

то для определения вещественной и мнимой частей надо умножить числитель и знаменатель (2.4.8) на число, комплексно-сопряженное знаменателю (т.е. на ). В результате получим

, (2.4.9)

где . (2.4.10)

Заметим, что не содержит мнимой единицы, имеющейся в записи (2.4.9). Если нужно найти модуль и аргумент дроби (2.4.8), то следует воспользо­ваться правилом (2.4.6), а не искать 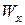и по (2.4.9) с последующим нахож­дением модуля и аргумента по (2.4.10).

Разложение на элементарные множители позволяет избежать ошибки оп­ределения аргумента без анализа, какой четверти принадлежит точка (ком­плексное число). Это иллюстрирует рис.2.4.2, на котором два вектора направ­лены противоположно и расположены в I и III четвертях, так что их аргументы и отличаются на . В то же время формально по формуле из (2.4.4) получим одну и ту же величину, равную . Имеем = + . Следова­тельно, формула (2.4.4) работает в I четверти. Если находить аргумент как сумму или разность аргументов векторов типа с и , то не ну­жен анализ, и результат получится без ошибки. Это особенно существенно, если аргумент больше, чем 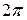и анализ четверти, в которой расположен вектор, не приведет к успеху.

Частотную передаточную функцию, или комплексный коэффициент уси­ления W(j), можно ввести двумя способами:

1. Путем нахождения реакции на синусоидальный (гармонический сигнал).

2. С помощью преобразования Фурье.

Начнем с первого способа и найдем реакцию системы (2.2.1) на гармониче­ский сигнал, который представим в показательной форме

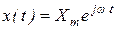, (2.4.11)

где Х_m и 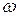- амплитуда и круговая частота.

Так как в линейной системе отсутствуют нелинейные искажения, то в ус­тановившемся режиме на выходе также будет гармонический сигнал той же частоты 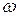, в общем случае с другими амплитудой и фазой, т.е.

. (2.4.12)

Для определения амплитуды и фазы подставим выражения сигна­лов (2.4.11), (2.4.12) и их производных в дифференциальное уравнение и после со­кращения на е^jt 0 и элементарных преобразова­ний получим тождество

. (2.4.13)

Отсюда 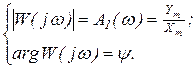(2.4.14)

Эти соотношения можно рассматривать как определение час­тотной пере­даточной функции. В них заключается физический смысл частотной переда­точной функции и из них вытекает способ её эк­спериментального нахождения путем измерения амплитуд гармоничес­ких сигналов на входе и выходе и сдвига по фазе между ними для одной и той же частоты.

В случае второго способа определения частотной передаточной функциисравним (2.4.13) и (2.2.15). Из сравнения следует, что час­тотная передаточная функция является частным случаем передаточ­ной функции по Лапласу

при р = j, т.е.

. (2.4.15)

Так как передаточная функция по Лапласу применима к сигналам произвольной (любой) формы, то и частотная передаточная функция применима для нахождения ре­акциина сигнал произвольной формы, а не обязательно гармонический. Из (2.4.5) для Фурье-изображения реакцииимеем

. (2.4.16)

Сама реакция, то есть оригинал, находится по формуле обращения

. (2.4.17)

Формула обращения позволяет трактовать сигнал как сумму элемен­тарных гармонических составляющих вида

, (2.4.18)

причем в соответствии с (2.4.18) и первым определением частотной передаточ­ной функции элементарная выходная гармоника равна про­изведению элемен­тарной входной гармоники на частотную передаточ­ную функцию при данной частоте.

Таким образом, из второго определения частотной передаточной функции вытекает частотный метод (метод преобразования Фурье) нахождения реак­ции:

1. Для заданного входного сигнала находим изображение по Фурье

. (2.4.19)

2. Находим Фурье-изображение реакции, используя (2.4.16)

Y(jw) = X(jw)×W(jw). (2.4.20)

3. По формуле обращения (обратного преобразования Фурье) находим реакцию . (2.4.21)

На практике для аналитически заданных x(t) и W(jw) операции (2.4.19) и (2.4.21) выполняются с помощью таблиц соответствия между оригиналами и изображениями. Если нет аналитических выражений или они сложны, то при­бегают к численным методам интегрирования (2.4.19), (2.4.21) с помощью ЭВМ.

Функция веса представляет собой (по определению) реакцию на -функцию. Следовательно, функция веса – это некоторый сигнал, а частотная передаточное функция – это изображение по Фурье этого сигнала. Поэтому одинаково, как по (2.4.21), так и по (2.4.30) можно объяснить смысл отрицатель­ных частот, трактуя сиг­нал - действительную функцию действительного аргу­мента t как сумму комплексных величин (гармоник) – элементарных векторов , вращающихся с круговой частотой на комплексной плоско­сти. Для получения в результате суммиро­вания действительного числа нужно, чтобы каждому элементарному вектору, вращающемуся против часовой стрелки (> 0), соответствовал элементарный вектор, вращающийся в противопо­ложном направлении (< 0). Тогда cyммa таких элементарных векторов по правилу параллело­грамма будет давать элементарный вектор, направленный вдоль вещественной оси, т.е. дей­ствительное чис­ло. Суммируя эти элементарные векторы, получим результирующий вектор, направленный по вещественной оси, т.е. действительный сигнал. Это иллюстрирует рис. 2.4.9.

Следовательно, отрицательные час­тоты представляют собой ма­тематическую абстракцию. Физическиих не суще­ствует. В резуль­тате изме­рения энергии сигнала в полосе частот от 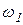до , т.е. на выходе полосового фильтра с полосой пропускания (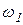, ), мы полу­чим величину, вдвое боль­шую по сравнению с теоре­тической величиной. Т.е. результат физического из­мерения надо разделить на два для абстрагирования к отрицательным частотам.

Заметим, что все реальные системы инерционны, т.е.имеют ограниченную полосу пропускания и

W(j) 0 при . (2.4.31)

Отсюда вытекает, что степень числителя передаточной функции (2.2.15) или (2.4.13) меньше степени знаменателя, т.е. m < n. Соответственно h (0) = 0.

Виды частотных характеристик.

Характер преобразования входного сигнала звеном или системой опреде­ляется частотной передаточной функцией или соответствующими ей частот­ными характеристиками. Виды частотных характеристик тесно связаны с фор­мами записи комплексных чисел, поскольку для 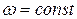частотная передаточ­ная функция является комплексным числом.

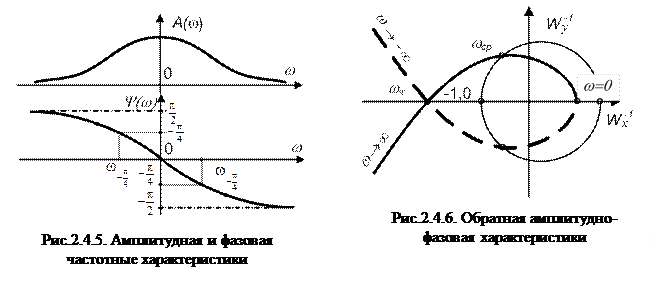
Перечислим теперь основные частотные характеристики (рис.2.4.3-2.4.6).

1. Амплитудно-фазовая характеристика (АФХ) – зависимость W(jw) на ком­плексной плоскости при изменении w от от -¥ до +¥ (Рис. 2.4.3). Так как W_х(w) = W_х(-w) – четная функция, а W_у(w) = W_у(-w) – нечетная функция, то АФХ для w < 0 симметрична относительно вещественной оси характеристике для w>0 и ее обычно не изображают.

2. Вещественная W_х(w) и мнимая W_у(w) частотные характеристики (рис. 2.4.4) – зависимости вещественной и мнимой части от частоты. Имея в виду четность вещественной характеристики и нечетность мнимой, их для w < 0 обычно не изображают. Четность W_х(w) и нечетность W_у(w) вытекают из правила (2.4.22) их выделения из W(jw), так как в знаменателе четная функция, а в числителе jw в четной степени – действительное число (отходит к W_х(w)), а в нечетной –мнимое (отходит к W_y(w)).

3. Амплитудная (АЧХ) и фазовая (ФЧХ) частотные характеристики – зависимости А(w) и y(w) от частоты (рис.2.4.5). В силу четности А(w) и нечетности y(w), их для w < 0 обычно не изображают. Амплитудная частотная характеристика определяет инерционность (пропускную способность) звена или системы. Фазовая частотная характеристика определяет величину фазового сдвига на соответствующей круговой частоте.

4. Обратная частотная характеристика W^-1(jw) = 1/ W(jw). Определяя амплитуду и аргумент (фазу) для дроби по правилу (2.4.6), найдем

. (2.4.22)

Из связи между формами записи комплексных чисел вытекает, что по АФХ можно построить W_х(w), W_у(w) или А(w), y(w), а также W^-1(jw) и наоборот. На рис.2.4.6 изображена обратная для характеристики на рис.2.4.3 характеристика. На рисунке построена окружность единичного радиуса. В соответствии с правилом (2.4.22) точки, соответствующие А(w) > 1, лежат внутри круга единичного радиуса. Точка А(w) = 1 остается на окружности, но фаза меняется на противоположную (на 180°).

Заметим, что реальные (физически реализуемые) звенья и системы имеют ограниченную полосу пропускания, т. е. А(w)® 0 при w ® 0 или W(jw) ® 0 при w ® ¥. Для выполнения этого условия в (2.4.13) должны иметь n > m, т. е. степень знаменателя передаточной функции должна быть больше степени чис­лителя.

Тем не менее, рассматриваются звенья, для которых условие физической осуществимости не выполняется. Это правомерно в определенном диапазоне частот. Если спектр сигнала на входе звена выходит за пределы этого диапазона, то возникнут искажения в реакции, не предусмотренные передаточной функцией звена.

5. Логарифмические частотные характеристики.

Наиболее широкое применение нашли логарифмические характеристики. Для их объяснения представим частотную передаточную функцию в показа­тельной форме и возьмем натуральный логарифм от :

.

Он равен комплексному выражению; вещественная его часть является лога­рифмом от модуля, а мнимая – фазой.

Вещественная часть логарифма представляет собой логарифмическую ам­плитудную характеристику, а мнимая часть – фазовую.

На практике берется десятичный логарифм, так что логарифмические ам­плитудная (ЛАХ) и фазовая (ЛФХ) характеристики определяются выраже­ниями: (2.4.23)

По оси абсцисс на графиках откладывается частота в логариф­мическом масштабе, т.е. lg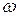. Однако желательно делать оцифров­ку непосредственно в значениях круговой частоты 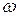, а для разметки можно воспользоваться табл.2.4.1.

Значения Таблица 2.4.1

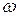
lg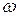		0.301	0.477	0.602	0.699	0.778	0.845	0.903	0.954

Амплитуда измеряется в децибелах, фаза – в градусах. Для разметки оси абсцисс непосредственно в значениях w (рад/с) можно воспользоваться любой из трех шкал (основной, квадратичной и кубической) логарифмической ли­нейки (рис.2.4.7).

Если взять за декаду D мм, то, например, 0.301 дек (соответствует 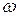= 2 рад/с) составит 0.301 D мм, 1.301 дек (соответствует 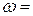20 рад/с) составит D +0.301 D мм и т.д. Таким образом, точки с оцифровкой в пределах от 1 до 10 сме­щаем вправо на декаду и оцифровываем от 10 до 100 и т.д. (рис.2.4.7), смещаем влево от исходного положения на одну декаду и оцифровываем от 0.1 до 1 и т.д.

Если w ₂ /w ₁ = 10, то расстояние между частотами равно одной декаде (lg 10=1), если w ₂ /w₁ = 2, то расстояние равно одной октаве.

Так как lg(w = 0 ) = -¥, то точка w = 0 находится на бесконечности слева. Поэтому ось ординат проводят в любом месте с таким расчетом, чтобы на гра­фик попал интересующий диапазон частот. Так как 20 lg 1 = 0, то L(w) > 0, если А(w)> 1 и L(w) < 0, если А(w) < 1. Если А(w)® 0, то L(w)® -¥.

Дата добавления: 2014-01-15