Вычисление двойных интегралов по теореме Фубини

Элементарное в направлении оси OY множество в 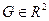может быть представлено в виде:

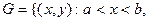
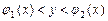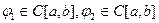},или

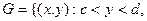
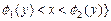- элементарное в направлении оси OX.

Для таких множеств в 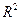формула (6) примет соответственно следующий вид:

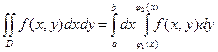. (9)

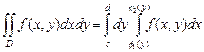. (10)

Интегралы, стоящие в правых частях равенств (9) и (10) называют повторными.

В правой части формулы (9) сначала вычисляют интеграл 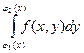, называемый внутренним, полагая 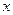постоянным. Затем производится интегрирование полученной функции по 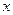. Аналогично в правой части формулы (8) сначала вычисляют внутренний интеграл 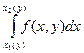, полагая 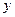постоянным, а затем производят интегрирование по 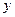. Такой способ вычислений определяется видом рассматриваемых множеств. Геометрически элементарное, например, в направлении оси OY множество представляется следую­щим образом: если интервал (a,b) есть проекция Dна ось ОХ, то для любой точки 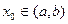прямая 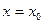, параллельная оси OY,пересекается с D по единственному интервалу 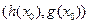, концы которого зависят от этой точки 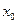. Утверждение, сформулированное в теореме Фубини (формула (9)), можно описать так: полагая х постоянным, берем интеграл по полученному в пересечении D и вертикальной прямой интервалу (вычисление внутреннего интеграла). Получаем некоторую функцию от x, которую интегрируем слева направо по интервалу изменения переменной x. Аналогичную геометрическую интерпретацию имеет повторный интеграл в правой части формулы (10).

Множество,элементарноев направлении осей ОХ и ОУ будем называть элементарным (простым) в .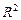

Если некоторое множество D не является элементарным в направлении ни одной из осей, чтобы вычислить по нему интеграл, представляют его в виде конечного объединения непересекающихся (без общих внутренних точек) множеств, замыкания которых будут элементарными в направлении оси OX или оси OY: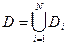. Тогда в силу свойства аддитивности интеграл по множеству D будет равен сумме интегралов по множествам, элементарным в направлении оси OX или OY:

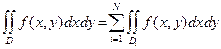
Замечание. Как следует из определения двойного интеграла, если 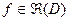и жорданово множество D симметрично относительно оси

OY, то из чётности функции 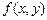по переменной x, т.е. из условия 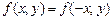, следует, что

.

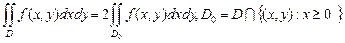Из нечётности функции 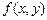по переменной x, т.е. из условия 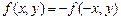, следует, что.

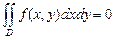Рассмотрим равенство повторных интегралов из правых частей формул (9) и (10):

=.

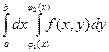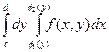Оно имеет место для множеств, замыкания которых есть множества, элементарные в направлении осей OX и OY. Переход от левой части этого равенства к правой и наоборот называется изменением порядка интегрирования в повторном интеграле.

Замечания. Обратите внимание на возможные ошибки!

· Пределы интегрирования во внешнем интеграле всегда константы, а пределы интегрирования во внутреннем интеграле, как правило, являются функциями.Пределы интегрирования внешнего и внутреннего интегралов могут быть константами только в том случае, если область интегрирования есть прямоугольник со сторонами, параллельными осям координат.

· В других случаях область интегрирования 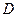разбивают на конечное число элементарных в направлениях осей OX или OY областей в зависимости от вида заданной области. Свойство аддитивности интеграла позволяет вычисление двойного интеграла по области 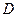свести к вычислению суммы интегралов по каждой из элементарных в направлении какой-либо оси областей.

· Если при некоторых значениях 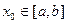функция, являющаяся нижним пределом в интеграле 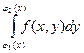формулы (9) принимает значение, большее, чем функция, являющаяся верхним пределом 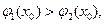то это ошибка. То же относится и к значениям функций 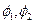в формуле (10). В этом случае следует проверить правильность составления чертежа области интегрирования.

· Ес­ли вместо функци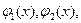й или 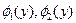поставить их значения в конце­вых точках 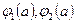или 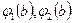б, то это ошибка.

· Если границы внутреннего интеграла в правой части формул (9) и (10) зависят не только от х, но и от у, то это ошибка.

· Если множество D симметрично относительно одной из ко­ординатных осей, но не дано условие четности функции f(x, у) относительно соответствующей переменной, то равенство

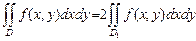
где 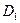часть множества D, лежащая по одну сторону от соответ­ствующей оси, вообще говоря, неверно.

Дата добавления: 2014-01-15