Вопросы для самопроверки. 1) Как определяется множество, элементарное в направлении оси OY ?

1) Как определяется множество, элементарное в направлении оси OY? оси OX? Какой вид имеет такое множество в плоскости XOY?

2) Как вычислить двойной интеграл по области 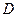, элементарной в направлении оси OY? Оси OX?

3) Как можно разбить область произвольного вида в плоскости XOY на части, каждая из которых будет элементарной в направлении оси OX или OY?

4) Как вычислить двойной интеграл по области произвольного вида в плоскости XOY?

Пример 2. 1)Изменить порядок интегрирования в интеграле.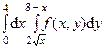

2) Вычислить 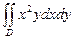, где D - область интегрирования из пункта 1).

Решение.

Y

8

C 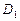A (4, 4)

0 4 X

Рис.1

1).a)В заданном повторном интеграле пределы внешнего интеграла по переменной 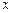равны 0 и 4. Это означает, что область интегрирования ограничена прямой x = 0 слева и прямой x =4 справа.

Пределы внутреннего интеграла по переменной 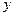указывают на то, что область ограничена снизу параболой 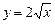и сверху прямой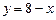. Построив все перечисленные линии, получим область и нтегрирования D(рис1.). Как видно из рисунка, область интегрирования является элементарной в направлении оси ОУ, но не является элементарной в направлении оси ОХ.

b) Для изменения порядка интегрирования область D разбиваем прямой 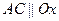на две области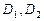, имеющие общую границу АС. Каждая область 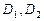будет элементарной в направлении оси ОХ, поэтому заданный интеграл будет равен сумме:

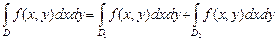
c) Выразим полученные двойные интегралы через повторные по формуле (9). Рассмотрим интеграл по 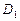. Как видно из рис.1, наименьшее значение, которое принимает 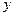в области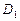, равно 0 в точке(0;0), а наибольшее значение равно 4 в точке (4;4). Следовательно, внешний интеграл по переменной 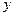по 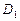будет иметь пределы: 0 и 4. Чтобы определить пределы внутреннего интеграла по переменной 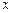, проведём мысленно прямую 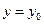, параллельную оси OX так, чтобы 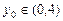. Тогда при движении слева направо (в направлении возрастания переменной 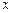), эта прямая будет «входить» в область, пересекая прямую 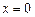, и «выходить» из области, пересекая параболу 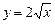. Получаем, что 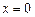- нижний предел. Из уравнения параболы 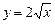получаем 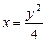- верхний предел. Таким образом, .

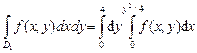d) В области 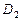наименьшее и наибольшее значения 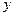соответственно равны 4 в точке(4;4) и 8 в точке (0;8). При движении вдоль прямой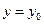слева направо, эта прямая «входит» в область, пересекая прямую 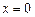, и «выходит» из области, пересекая прямую 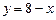. Получаем, что 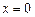- нижний предел. Из уравнения 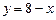получаем 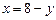- верхний предел. Тогда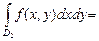 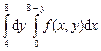и общий результат:

=+.

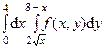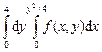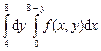2) По формуле (9) получим

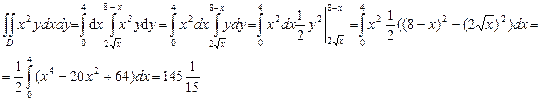
Задание 2

Изменить порядок интегрирования в следующих повторных интегралах:

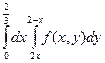
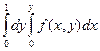
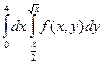
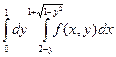
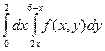
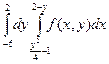
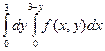
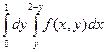
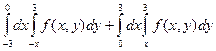
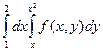
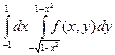
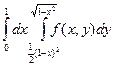
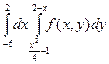
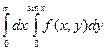
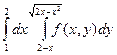
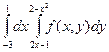
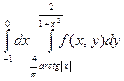
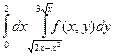
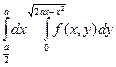
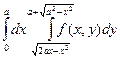
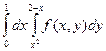
Задание3

Вычислить двойные интегралы по области 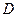, разбивая её при необходимости на области, элементарные в направлении оси OX или OY:

	Двойной интеграл	Уравнения кривых, ограничивающих область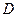
		, ,
		, ,
		, ,
		, ,
		, ,
		,
		, ,
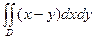
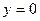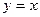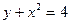
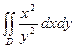
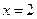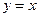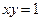
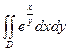
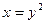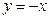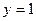
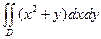
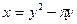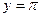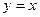
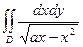
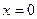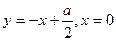
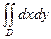
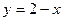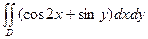
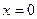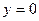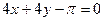
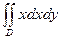
		треугольник с вершинами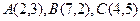
		, ,
		,
		,
		, , ,
		, , ,
		,

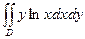
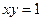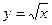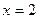
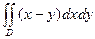
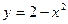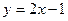
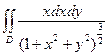
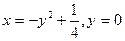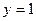
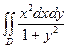
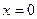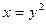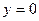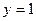
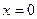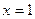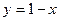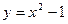
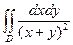
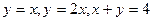
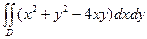
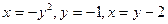
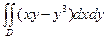
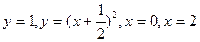
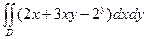
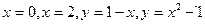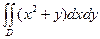
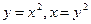
Дата добавления: 2014-01-15