Условие Стодолы

Для устойчивости необходимо и достаточно, чтобы все корни характеристического уравнения располагались в левой полуплоскос­ти.

Необходимость условия устойчивости. Необходимость заключается в том, что если система устойчивая, то корни характеристического уравнения имеют строго отрицательные вещественные части, т.е. находятся в левой комплексной полуплоскости.

Достаточность условия устойчивости. Достаточность заключается в том, что наличие всех корней характеристического уравнения с отрицательными вещественными частями гарантирует устойчивость, согласно формуле (2.9.1.).

Строгое общее опреде­ление устойчивости, методы исследования устойчивости нелинейных систем и возможность распространения заключения об устойчивости линеаризованной системы на исходную нелинейную систему даны рус­ским ученым А.М.Ляпуновым.

На практике устойчивость часто определяется косвенным пу­тем, с помощью так называемых критериев устойчивости без непос­редственного нахождения корней характеристического уравнения. К ним относятся алгебраические критерии: условие Стодолы, критерии Гурвица, Михайлова, а также частотный критерий Найквиста. При этом критерий Найквиста позволяет определять устойчивость замкнутой системы по АФХ или по логарифмическим характеристикам разомкнутой системы.

Условие получено словацким математиком Стодолой в конце 19-го столетия. Оно интересно в методическом плане для понимания условий устойчивости системы.

Запишем характеристическое уравнение системы в виде

D(p) = a₀pⁿ + a₁p^{n- 1} +…a_n= 0. (2.9.3)

По Стодоле для устойчивости необходимо, но недостаточно, чтобы пpи a₀ > 0 все остальные коэффициенты были строго положительны, т.е.

a₁ > 0,..., a_n > 0.

Необходимость можно сформировать так:

Если система устойчива, то все корни характеристического уравнения имеют 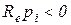, т.е. являются левыми.

Доказательство необходимости элементарное. По теореме Безу характеристический полином можно представить в виде

.

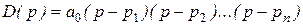Пусть 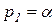, т.е действительное число, а 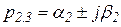– комплексно-сопряженные корни. Тогда

…

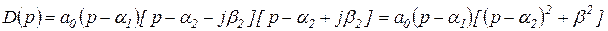Отсюда видно, что в случае полинома с действительными коэффициентами 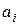комплексные корни попарно-сопряженные. При этом, если 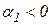, , 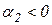то имеем произведение многочленов с положительными коэффициентами, которое дает многочлен только с положительными коэффициентами.

Недостаточность условия Стодолы заключается в том, что условие 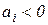не гарантирует, что все 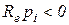. В этом можно убедиться на конкретном примере, рассмотрев полином степени .

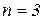Заметим, что в случае 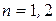условие Стодолы одновременно необходимо и достаточно. Из 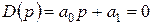вытекает 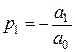. Если 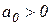, то и , чтобы .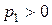

Для 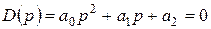из анализа формулы корней квадратного уравнения также вытекает достаточность условия.

Из условия Стодолы вытекает два важных следствия.

1. Если условие выполняется, а система неустойчива, то переходный процесс имеет колебательный характер. Это следует из того, что уравнение с положительными коэффициентами не может иметь действительных положительных корней. По определению корень – это число, обращающее характеристический полином в нуль. Никакое положительное число не может обратить в нуль многочлен с положительными коэффициентами, то есть быть его корнем.

2. Положительность коэффициентов характеристического полинома (соответственно выполнение условия Стодолы) обеспечивается в случае отрицательной обратной связи, т.е. в случае нечетного числа инверсий сигнала по замкнутому контуру. В этом случае характеристический полином 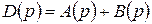. В противном случае имели 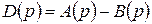и после приведения подобных некоторые коэффициенты могли оказаться отрицательными.

Заметим, что отрицательная обратная связь не исключает возможности невыполнения условия Стодолы. Например, если 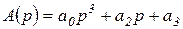, а , то в случае единичной отрицательной обратной связи . В данном полиноме коэффициент при 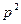равен нулю. Отрицательных коэффициентов нет, но, тем не менее, условие не выполняется, так как оно требует строго выполнения неравенств .

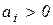Это подтверждает и следующий пример.

Пример 2.9.1. Применить условие Стодолы к схеме рис. 2.9.2.

Передаточная функция разомкнутой по цепи единичной отрица­тельной обратной связи системы равна 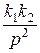и характеристичес­кое уравнение замкнутой системы есть сумма числителя и знаменателя, т. е.

D(p) = p ² + k ₁ k ₂ = 0.

Так как отсутствует член с р в первой степени (a ₁ = 0), то условие Стодолы не выполняется и система неустойчива. Данная система структурно неустойчива, так как ни при каких значениях параметров k ₁ и k ₂ не может быть устойчивой.

Чтобы сделать систему устойчивой, нужно ввести дополнительную связь или корректирующее звено, т.е. изменить структуру системы. Покажем это на примерах. На рис. 2.9.3. звено прямой цепи представлено последовательно включенными звеньями с передаточными функциями и . Параллельно первому введении дополнительная связь.

Передаточная функция разомкнутой по единичной отрицательной связи системы и характеристическое уравнение замкнутой системы соответственно равна

,

.

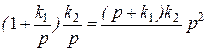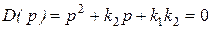Теперь условие Стодолы выполняется при любых 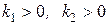. Так как в случае уравнения второй степени оно не только необходимо, но и достаточно, то система устойчива при любых положительных коэффициентах усиления .

На рис.2.9.4 в схему введено последовательно форсирующее звено. Передаточная функция разомкнутой по цепи единичной отрицательной связи системы в этом случае равна 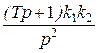и характеристическое уравнение замкнутой системы равно

.

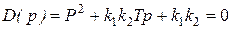Аналогично предыдущему система устойчива при любых положительных .

Дата добавления: 2014-01-15