
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теория прочности Мора
|
|
|
|
В отличии от рассмотренных выше классических теорий, используется не один, а два критерия: нормальное и касательное напряжения. Окончательно теория сформулирована Отто Мором20 в 1900 году. В ее основании лежит логическое описание явления перехода материала в предельное состояние с помощью кругов напряжений. Из трех кругов напряжений (рис. 6.5) учитывается только наибольший, построенный на отрезке [ σ 1, σ 3] как на диаметре в координатных осях σ и τ.
Предположим, что задано некоторое напряженное состояние, для которого можно вычертить наибольший круг напряжений. Если увеличивать пропорционально одному параметру все компоненты, то рано или поздно напряженное состояние станет предельным, для которого и строится круг предельных напряжений. Теперь допустим, что проведено большое число испытаний при различных напряженных состояниях и для каждого из них установлено предельное состояние. В результате можно построить семейство кругов предельных состояний, к которым вычерчивается огибающая линия предельных кругов Мора, которая считается единственной для данного материала. Практически, вместо огибающей, используется её схематизированное приближение, построяемое на основе экспериментов с образцами материала при одноосном растяжении и сжатии. огибающая линия при этом заменяется касательной к предельным кругам Мора при растяжении (круг В) и при сжатии (круг С), отвечающим результатам названных испытаний (рис. 6.5).
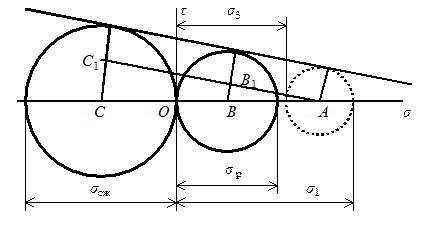
Рис. 6.5. Касательная кругов Мора, играющая роль огибающей линии.
Далее необходимо найти величину эквивалентного напряжения, соответствующего теории Мора. С этой целью будем считать, что для исследуемого материала схематизированная огибающая кругов Мора задана в виде касательной к кругам B и С. Найдем зависимость между главными напряжениями σ 1 и σ 3 заданного предельного напряженного состояния (состояния А, показанного пунктиром на рис. 6.5) и равно опасного ему одноосного состояние растяжения.
Восстановим перпендикуляры, в точках касания трех кругов с касательной к ним, которые совпадут с радиусами этих кругов (см. рисунок). Из точки A проведем прямую АС 1, параллельную касательной. Из подобия треугольников АСС 1 и АВВ 1 следует:
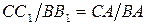 . (a)
. (a)
Из того же рисунка непосредственно следует, что:
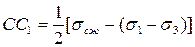 ,
, 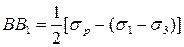 ,
,
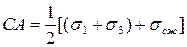 ,
, 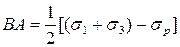 , (b)
, (b)
где σ ри σ сж –– предельные напряжения материала при растяжении и сжатии.
Подставив выражения (b) в равенство (a), после упрощений получим:

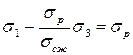 . (c)
. (c)
Обозначим: как 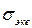 — левую часть равенства (c),
— левую часть равенства (c), 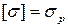 и отношение
и отношение 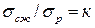 . Тогда условие прочности, записанное согласно теории прочности Мора, примет вид:
. Тогда условие прочности, записанное согласно теории прочности Мора, примет вид:
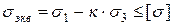 , (6.10)
, (6.10)
где [ σ ] — допускаемое напряжение материала при одноосном растяжении. Если материал пластичен и одинаково сопротивляется растяжению и сжатию, то, приравнивая σ сж величине σ р, получим 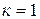 и выражение (6.10) в этом случае совпадет точно с выражением (6.5), полученном нами ранее, при рассмотрении 3-й теории прочности.
и выражение (6.10) в этом случае совпадет точно с выражением (6.5), полученном нами ранее, при рассмотрении 3-й теории прочности.
Теория Мора в настоящее время считается общепризнанной. Она оправдывает себя как для пластичных, так и для хрупких материалов, но, преимущественно, для напряженных состояний смешанного типа, то есть когда отношение 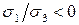 . Отличительной чертой теории Мора от рассмотренных ранее классических теорий является тот факт, что она полностью опирается на экспериментальные данные и по мере их накопления может уточняться. Основные недостатками теории Мора:
. Отличительной чертой теории Мора от рассмотренных ранее классических теорий является тот факт, что она полностью опирается на экспериментальные данные и по мере их накопления может уточняться. Основные недостатками теории Мора:
Первое, это отсутствие влияния промежуточного главного напряжения σ 2 (как и в третьей теории).
Второй недостаток — это трудности в связи с построением огибающей линии предельных кругов Мора.
15 Галилей Галилео (1564 — 1642) — итальянский физик, механик, астроном, математик. В его сочинениях (1638) содержатся вопросы, касающиеся: прочности растянутых и изгибаемых брусьев, геометрически подобных тел, балок равного сопротивления и др.
16 мариотт Эдм (1620 –– 1684) –– французский ученый, изучавший прочность материалов и их упругие свойства. Исходил из теории прочности, критерием разрушения в которой является достижение материалом предельного удлинения. Получил формулу для определения прочности труб на разрыв под действием внутреннего давления.
17 Кулон Шарль Огюстен (1736 –– 1806) –– французский ученый. Занимался испытанием материалов на растяжение, срез и изгиб. Он имел ясное представление о распределении внутренних сил по поперечному сечению.
18 Бельтрами Эудженно (1835 — 1900) — итальянский математик.
20 См. в сноске 13.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 3674; Нарушение авторских прав?; Мы поможем в написании вашей работы!