Состояние покоя механической системы может быть устойчивым, неустойчивым и безразличным

СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ В КОНСЕРВАТИВНОМ СИЛОВОМ ПОЛЕ

ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ СОСТОЯНИЯ ПОКОЯ МЕХАНИЧЕСКОЙ

СИСТЕМЫ. ТЕОРЕМА ЛАГРАНЖА-ДИРИХЛЕ.

ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ СОСТОЯНИЯ ПОКОЯ МЕХАНИЧЕСКОЙ

Лекция IV-ОАМ-17

Состояние покоя механической системы называется устойчивым, если эта система, выведенная из положения покоя, совершает колебания около этого положения.

Состояние покоя механической системы называется неустойчивым, если при сколь угодно малом отклонении системы из положения покоя она удаляется от этого положения и колебаний около этого положения не возникает.

Состояние покоя механической системы называется безразличным, если при отклонении ее из этого положения она и в новом положении может оставаться в состоянии покоя.

Критерий устойчивости состояния покоя для систем с голономными и стационарными связями, находящихся в консервативном силовом поле, устанавливается в зависимости от потенциальной энергии этих систем. Представим себе механическую систему с голономными стационарными связями, находящуюся под действием сил, имеющих потенциал. Такую систему, как указывалось выше (§ 72), называют консервативной.

Для консервативной системы уравнения равновесия сил имеют вид (121.7):

.

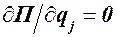
Из уравнений (121.7) следует, что положениям покоя консервативной системы соответствуют экстремальные значения потенциальной энергии системы.

Однако по уравнениям равновесия сил (121.7) нельзя судить об устойчивости состояния покоя в этих положениях системы. Условие устойчивости состояния покоя механической системы содержится в теореме Лагранжа-Дирихле. Эта теорема устанавливает, что те положения покоя консервативной системы, в которых потенциальная энергия системы достигает минимума, являются ее устойчивыми состояниями покоя.

Для консервативной системы с одной степенью свободы положения покоя определяются одним уравнением:

(123.1)

Чтобы определить, устойчиво ли состояние покоя в рассматриваемом положении системы, необходимо выяснить, имеет ли потенциальная энергия системы в этом положении минимум.

В том случае, если 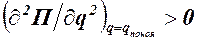(123.2)

Дата добавления: 2014-01-15