То условие минимума выполнено.

Если же 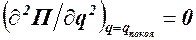, то, следовательно, вторая производная не может служить критерием минимума потенциальной энергии.

В этом случае необходимо вычислить последовательные производные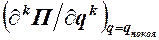

Если первая, не равная нулю, производная имеет четный порядок и при этом положительна, то при 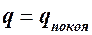потенциальная энергия имеет минимум, а, следовательно, это положение покоя системы устойчиво.

Если же первая, не равная нулю, производная имеет нечетный порядок, то при 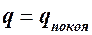нет ни максимума ни минимума.

Критерий Лагранжа-Дирихле является достаточным (но не необходимым) условием устойчивости состояния покоя системы в поле консервативных сил.

Рассмотрим теперь вопрос о том, как оценить состояние покоя консервативной системы в положении, в котором она не имеет минимума потенциальной энергии. Ответ на этот вопрос содержится в специальных теоремах А. М. Ляпунова¹.

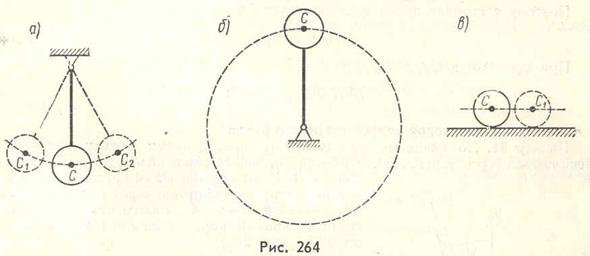
На рис. 264, а изображено положение покоя физического маятника, соответствующее наинизшему положению его центра тяжести. В этом положении потенциальная энергия маятника в поле силы тяжести имеет минимум и это состояние покоя является устойчивым. Если вывести маятник из этого положения, отклонив его на некоторый угол в вертикальной плоскости, то он начнет качаться вокруг оси привеса.

На рис. 264, б изображен маятник в том положении, при котором его центр тяжести занимает наивысшее положение. В этом положении потенциальная энергия маятника имеет максимум, и это состояние покоя является неустойчивым. И если вывести маятник из этого положения, то он не возвратится в первоначальное положение.

На рис. 264, в изображен шарик, находящийся на горизонтальной плоскости. Состояние покоя шарика является безразличным. Потенциальная энергия шарика в любом положении на плоскости не имеет ни минимума, ни максимума, являясь постоянной величиной, не изменяющейся при изменении положения шарика.

Вопросы для самоконтроля

1. Каков вид условий равновесия сил, имеющих потенциал?

2. Каким может быть состояние покоя механической системы?

10. Каков критерий устойчивости состояния покоя механической системы,
устанавливаемый теоремой Лагранжа- Дирихле?

11. Как установить вид состояния покоя механической системы с одной степенью свободы в том случае, если ?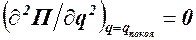

12. Каков порядок исследования состояния покоя механической системы на
устойчивость?

Дата добавления: 2014-01-15