Дифференциальные уравнения. Опр.Обыкновенным дифференциальным уравнением n-ого порядка называется соотношение вида:

Опр. Обыкновенным дифференциальным уравнением n-ого порядка называется соотношение вида:

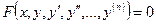
К обыкновенным дифференциальным уравнениям приводят многие задачи физики, химии естествознания, политологии для исследования поведения различных систем.

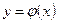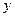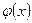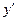Опр. Функция называется решением этого дифференцированного уравнения, если после замены на 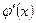, 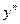на ,……,на уравнение обращается в тождество.

В обыкновенных дифференциальных уравнениях неизвестная функция зависит только от одного аргумента.

Опр. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение

Пример:

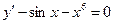– 1-ого порядка

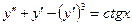– 2-ого порядка

будем считать что рассматриваемые величины принимают действительные конечные значения, а рассматриваемые функции однозначны.

Пример:

Известно, что скорость распада радия прямо пропорциональна количеству радия; допустим что в момент времени 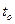имелось 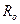грамм радия. Требуется определить количество 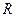радия в любой момент времени 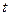. Обозначим коэффициент пропорциональности .

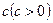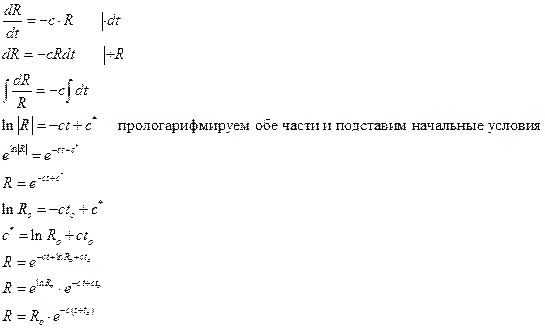
Одному и тому же уравнению могут удовлетворять очень многие функции. Для определения исходной функции задаются начальные условия, которые единственным образом определяют соответствующее им решение дифференциального уравнения.

Основной задаче теории дифференциальных уравнений является разыскание всех решений данного дифференциального уравнения и изучение свойств этих решений.

Нахождение решений дифференциального уравнения называется интегрированием этого уравнения.

Опр. Дифференциальное уравнение первого порядка имеет вид.

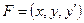
или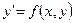

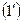
Дата добавления: 2014-01-15