Теорема существования и единственности

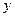Если в уравнении (1’) функция и непрерывны по в некоторой области , содержащей точку , то существует единственное решение этого уравнения 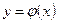, удовлетворяющее начальным условиям:

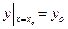(2)

Геометрический смысл теоремы:

существует и притом единственная функция 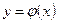, график которой проходит через точку.

Если начальные условия не заданы, то уравнение имеет бесконечное множество решений.

Опр. Общим решением дифференциального уравнения 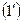называется функция 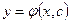зависящая от произвольной постоянной 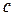и удовлетворяющая условиям:

1) функция удовлетворяет уравнению 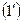при любых конкретных значениях постоянной

2) каково бы ни было н.у. 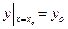можно найти такое , что функция удовлетворяет н.у. (2)

Опр. Равенство вида неявно задающее общее решение 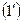называется общим интегралом дифференциального уравнения

Частным решением 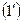называется любая функция , которая получена из общего решения, если в последнем произвольной постоянной 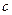придать определенное значение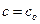

Задача, нахождения частного решения удовлетворяющего н.у. 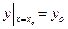называется задачей Коши.

Соотношение 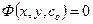называется частным интегралом.

Геометрический смысл.Общий интеграл представляет собой семейство кривых на координатной плоскости, зависящее от одной произвольной постоянной 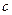. Эти кривые называются интегральными кривыми данного дифференциального уравнения.

Частному интегралу соответствует одна кривая этого семейства, проходящая через некоторую заданную точку плоскости.

Геометрический смысл дифференциального уравнения 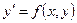где определена в некоторой области

Уравнение определяет в любой точке плоскости угловой коэффициент наклона касательной к интегральной кривой, проходящей через эту точку.

Если в каждой точке 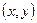области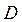представить с помощью некоторого отрезка направление касательной, определяемое значением , то получим поле направлений.

Задачу нахождения решения уравнения 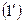можно переформулировать так: требуется найти кривую 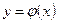, которая в любой своей точке имеет заданную уравнением 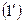касательную, т.е. поле направлений.

Уравнения с разделяющимися переменными

Это уравнения вида:

Решается растаскиванием в разные части уравнения функции с одинаковыми неизвестными

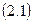
Частный случай:

I.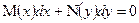

II.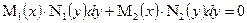

Это уравнение может быть приведено к уравнению с разделяющимися переменными дел. на

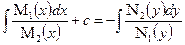
Решение простейших дифференциальных уравнений методом разделения переменных

1).

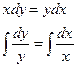
константу интегрирования запишем в виде 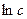, так удобнее

Напоминание: - основновное логарифмическое тождество

потенцируем, т.е возводим 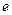в степени, равные левой и правой части равенства

т.к. основанием натурального логарифма является 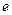, то на основании логарифмического тождества получим:

__________________________

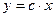
2).

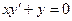
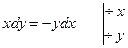
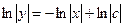
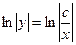
потенцируем

__________________________

3).

__________________________

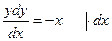
4).

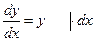
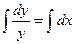
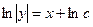
потенцируем

__________________________

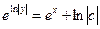
5).

__________________________

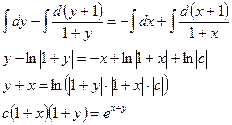
Решить задачу Коши

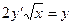
6). (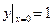- другая форма записи начального условия)

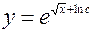
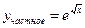
Решить задачу Коши н.у.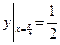

7).

__________________________

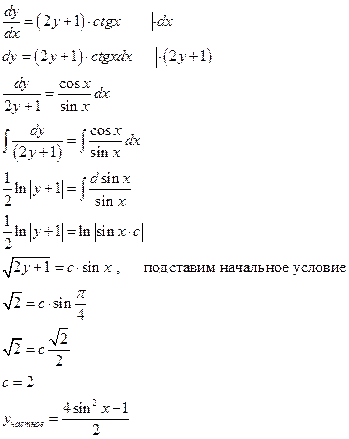
8).

__________________________

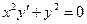
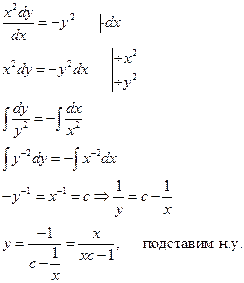
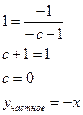
Решить дифференциальное уравнение

9).

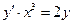
потенцируем

__________________________

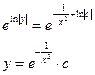
10).

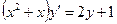
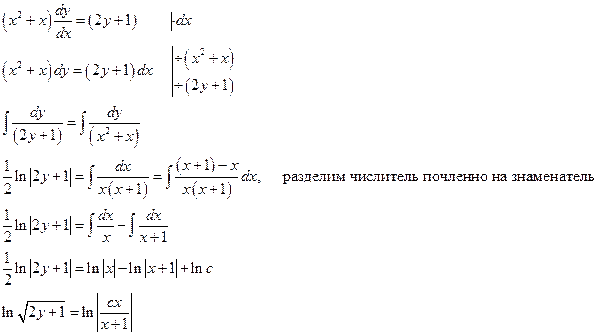
потенцируем

__________________________

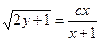
11).

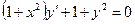
берем 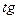от обеих частей, т.к.

__________________________

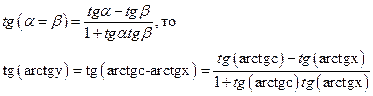
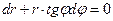
12). 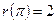- начальное условие

__________________________

13).

__________________________

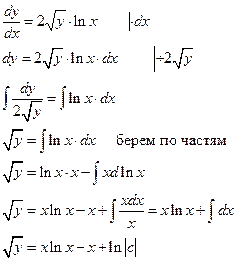
14).

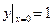
Дата добавления: 2014-01-15