Пространственная графика

Обратимся теперь к трехмерное случаю (3D) (3-dimension) и начнем рассмотрение сразу с введения однородных координат.
Поступая аналогично тому, как это было сделано в размерности два, заменим координатную тройку (х, у, z), задающую точку в пространстве, на четверку чисел (х у z 1) или, в более общем виде, на четверку
(hx hy hz h), h 0.

Каждая точка пространства (кроме начальной точки О) может быть задана четверкой одновременно не равных нулю чисел; эта четверка чисел определена однозначно с точностью до общего множителя.
Предложенный переход к новому способу задания точек дает возможность воспользоваться матричной записью и в более сложных, трехмерных задачах.
Любое аффинное преобразование в трехмерном пространстве может быть представлено в виде суперпозиции вращений, растяжений, отражений и переносов. Поэтому имеет смысл подробно рассмотреть матрицы именно этих преобразований (очевидно, что в данном случае порядок матриц должен быть равен четырем).

В. Матрицы вращения в пространстве
Матрицы вращения вокруг оси абсцисс, ординат и аппликат соответственно будут иметь вид:

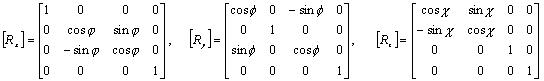
Полезно обратить внимание на место знака "-" в каждой из трех приведенных матриц.
Г. Матрицы отражения относительно плоскостей хy, уz, zx, соответственно:

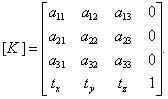
Как и в двумерном случае, все описанные матрицы невырождены.
Таким образом, результирующая матрица преобразований в пространстве будет иметь вид:К

Очевидно, что для изменения положения некоторого тела в пространстве необходимо выполнить преобразование координат для каждой его точки.

Дата добавления: 2014-01-15