Допускающие понижение порядка

Дифференциальные уравнения высших порядков,

1⁰. Уравнение вида y ⁽ⁿ⁾ = f(x) решается последовательным n-кратным интегрированием правой части. При каждом интегрировании получается одно произвольное постоянное, а в окончательном результате – n произвольных постоянных.

Пример. Решить уравнения:

1) .

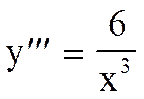Последовательно интегрируя, получим:

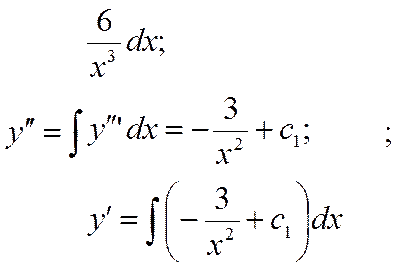
2)

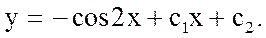
2⁰. Если в уравнение не входит искомая функция y, то есть он имеет вид 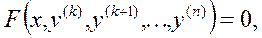то порядок уравнения можно понизить, взяв за новую неизвестную функцию низшую из производных, входящую в уравнение, т.е. сделав замену

Пример 1. Уравнение вида не содержит явным образом искомой функции y.

Решение. Обозначим производную 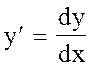через Р, т.е. положим 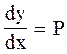. Тогда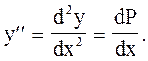

Подставляя эти выражения производных в исходное уравнение, получим уравнение первого порядка

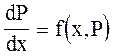
относительно неизвестной функции Р от х. Проинтегрировав это уравнение, найдем его общее решение:

а затем из соотношения получим общий интеграл исходного уравнения:

Пример 2. Решить уравнение

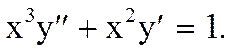
Положим 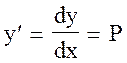, тогда 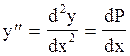и мы получаем дифференциальное уравнение первого порядка относительно вспомогательной функции Р от х:

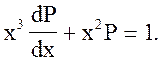
Поделив уравнение на х³, получим

-

линейное дифференциальное уравнение первого порядка. Представим функцию Р в виде 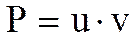, тогда

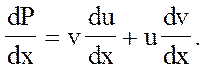
Подставляя их в уравнение, получим

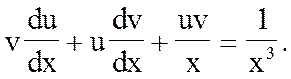
Далее

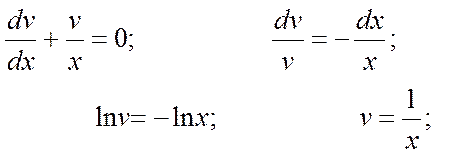
отсюда 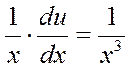или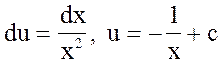

.

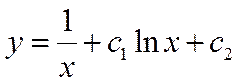3⁰. Если в уравнение не входит независимая переменная х, т.е. уравнение имеет вид то порядок уравнения можно понизить, взяв за новое независимое переменное y, а за неизвестную функцию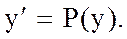

Пример. Решить уравнение

В уравнение не входит х. Полагаем 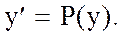Тогда

Подставляя 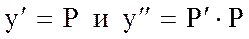в уравнение, получим:

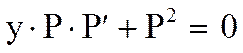или ,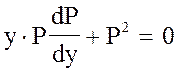

откуда

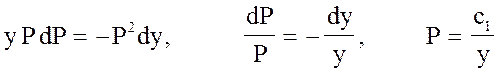
или

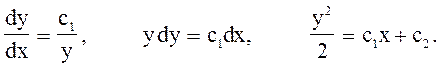
Дата добавления: 2014-01-15