Лекция № 1, ВАС-11, 2 семестр

Состав курса

Ростов-на-Дону,

Математика

В.В. Трофимов

Лекции по интегральному исчислению
функции одной переменнрй
для студентов первого курса,
II семестра вечернего отделения

Курс лекций II семестра включает в себя следующие разделы интегрального исчисления.

1⁰. Первообразная функция, неопределенный интеграл и его свойства.

2⁰. Методы вычисления неопределенных интегралов.

3⁰. Определенный интеграл, классы интегрируемых функций, основные свойства определенного интеграла, формула Ньютона-Лейбница.

4⁰. Методы вычисления определенных интегралов.

5⁰. Геометрические и механические приложения определенного интеграла.

6⁰. Численные методы интегрирования.

Тема. Первообразная функция, основные свойства. Неопределенный интеграл, его свойства. Таблица основных интегралов. Метод непосредственного интегрирования функций.

1. Первообразная функция, неопределенный интеграл
и его свойства

В математике выделяют прямые и обратные задачи. Примерами обратных задач являются знакомые нам из школьного курса задача нахождения неизвестного слагаемого по сумме и известному слагаемому, а также задача нахождения неизвестного сомножителя по произведению и известному сомножителю:

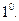
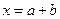– прямая задача,

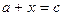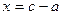, – обратная задача;

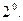
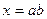– прямая задача,

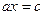, – обратная задача.

В математическом анализе задачей, обратной дифференцированию, является задача интегрирования. В прямой задаче по известной функции находят ее производную, в обратной задаче по известной производной находят саму функцию.

Рассмотрим примеры таких задач.

1. Прямая задача. Дана функция 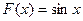. Найти ее производную 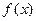. Решение задачи: .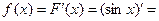

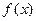
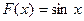Обратная задача. Известно, что производная некоторой функции равна . Найти функцию . Решение задачи: , так как 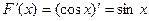. Функция 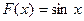является первообразной для функции

2. Прямая задача. Дана функция . Найти ее производную 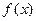. Решение задачи: .

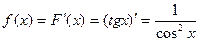1⁰. Обратная задача. Известно, что производная некоторой функции равна . Найти функцию .

2⁰. Решение задачи: , так как 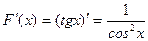. Функция 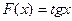– первообразной для функции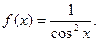

Определение 1.1. Функция называется первообразной для функции 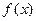на некотором промежутке, если на всем этом промежутке 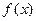является производной для функции ,

. (1.1)

Рассмотрим две теоремы, выражающие важнейшие свойства первообразной функции.

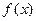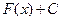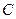Теорема 1.1. Если на некотором промежутке функция является первообразной для функции , то и функция , где – любая постоянная, также является первообразной для функции 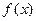на этом промежутке.

Доказательство. В самом деле, пусть – первообразная функция для функции 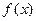, тогда . Но 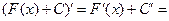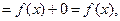и утверждение доказано.

Функция 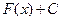называется семейством первообразных функций для функции 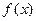. Например, семейством первообразных функций для функции 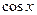является семейство функций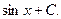

Возникает естественный вопрос: достаточно ли найти какую-либо одну первообразную для функции 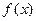, чтобы получить все первообразные? Ответ на этот вопрос дает следующее свойство первообразной функции в совокупности с первым свойством (примем его без доказательства).

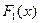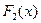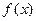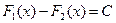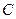Теорема 1.2. Пусть функции и – две первообразные для функции на некотором промежутке, тогда на этом промежутке , где – любая постоянная.

Мы установили важный: если функция является первообразной для функции 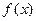на некотором промежутке, то любая другая первообразная функция 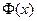может отличаться от функции на данном промежутке только на константу С. Таким образом, все первообразные для функции 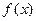на этом промежутке имеет вид:

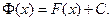(1.2)

Множество (семейство) функций (1.2) носит название неопределенного интеграла для функции .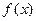

Определение.1.2. Пусть функция является первообразной для функции 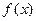на некотором промежутке, тогда выражение 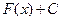называется неопределенным интегралом на этом промежутке и обозначается символом 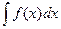. Таким образом,

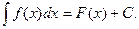(1.3)

Функцию 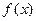называют подынтегральной функцией, выражение 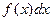– подынтегральным выражением, 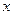– переменной интегрирования, знак 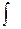– знаком интеграла.

Дата добавления: 2014-01-15