Эмпирическая функция распределения

Эмпирическая функция распределения. Графическое представление статистических рядов.

Пусть известно статистическое распределение ча­стот количественного признака X. Введем обозначения: 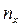- число наблюдений, при которых наблюдалось значение признака, меньшее x; n – общее число наблюдений (объём выборки).

Очевидно, что относительная частота события 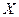< x равна: 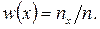Из данного выражения видно, что относительная частота 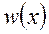является функцией заданного значения x, так как действительно – если x изменяется, то изменяется и относительная частота (частость).В связи с тем, что относительная частота определяется лишь после проведения испытаний (опыта, эксперимента), то она, как принято говорить, находится эмпирическим (опытным) путём. Поэтому её (функцию 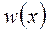)называютэмпирической.На этом основании в статистикевводят понятие эмпирической функции распределения

Эмпирической функцией распределения (функцией распределения выборки) называют функцию 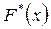, определяющую для каждого значения x относительную частоту события 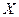< x.

Таким образом, в соответствии с данным определением:

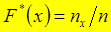(3.1)

где 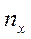- число вариант, меньших x; n – объём выборки.

Следовательно,для того чтобы найти, например, 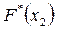, надо число вариант, меньших x₂, разделить на объём выборки:

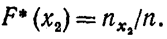(3.2)

В отличие от эмпирической функции распределения выборки 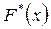функцию распределения генеральной совокупности 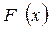называюттеоретической функцией распределе­ния. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция 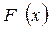определяет вероятность события 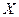< x ,а эмпирическая функция 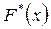определяет относительную частоту этого же события.

Из теоремы Бернулли следует, чтоотносительная частота события 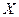< x, т.е. 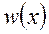= 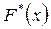стремится к вероятности 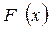этого события. Другими словами - при больших объёмах выборки, т.е. числа «n», числа 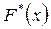и 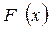мало отличаются одно от другого, так как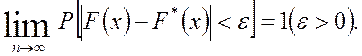

На основании данного соотношения, следует целесообразность использования эмпирической функции распреде­ления выборки для приближенного представлениятеоре­тической (интегральной) функции распределения гене­ральной совокупности.

Данный вывод подтверждается тем, что эмпирическая функция распределения 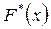обладает всеми свойствамитеоретической функции распределения 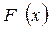. Действительно,из определенияэмпирической функции распределения 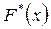вытекают следующие её свойства:

1) значения эмпирической функции принадлежат отрезку ;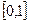

2) 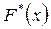- неубывающая функция;

3 ) Если x₁ – наименьшая варианта, то 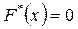при 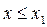; если же 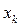- наибольшая варианта, то 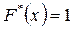при .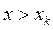

И так, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример. Построить эмпирическую функцию по данному распре­делению выборки:

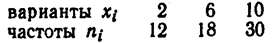Решение.

Найдём объём выборки: n = 12+18+30=60.

Из условия примера видно, чтонаименьшая варианта (наблюдаемое значение x ) равна 2. Тогда:

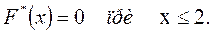
Значение вариант 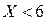, наблюдалось лишь один раз, а именно значение , причём частота этой варианты 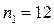. Следовательно:

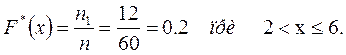
Значения вариант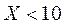, а именно 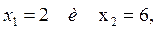наблюдалось 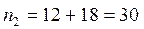раз. Следовательно:

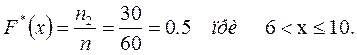
Наибольшая варианта(наблюдаемое значение x ) равно 10, тогда:

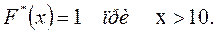
Таким образом, искомая эмпирическая функция, по условию примера, равна:

График искомой эмпирической функции распределения имеет вид, представленный на Рис.3.1.

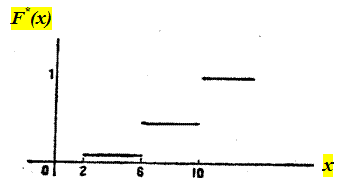Рис.3.1 График искомой функции распределения примера.

Дата добавления: 2014-01-15