Алгебри. Структури. Булеві алгебри

Розділ ІІ. Булева алгебра.

Означення 1. Алгеброю A називається сукупність множини М з зада­ними на ній операціями 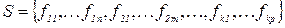, позначається: A =. Множина М називається носієм алгебри, а сукупність операцій S - сигнату­рою алгебри. В позначенні операції f_mp перший індекс вказує на кількість місць операції.

Означення 2. Алгебра A =, сигнатура якої складається з однієї бінарної операції f, називається групоїдом.

Бінарні операції поділяються на два типи, а саме: операції типу додавання (надалі будемо позначати); операції типу множення (надалі будемо позначати*).

Групоїд називається адитивним. Групоїд 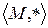називається мультиплікативним.

Означення 3. Нехай A =- групоїд. Елемент називається нейтральним елементом, якщо для довільного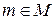виконується рівність .

Групоїд не може мати більше одного нейтрального елемента. Дійсно, нехай 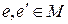два нейтральних елементи. Тоді .

Якщо групоїд мультиплікативний, то нейтральний елемент називається одиницею і позначається 1, якщо групоїд адитивний, то нейтральний елемент називається - нулем і позначається 0.

Означення 4. Групоїд A =називається ідемпотентним, якщо операція задовольняє закону ідемпотентності:для довільного , .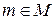

Означення 5. Групоїд A =, в якому виконується закон асоціа­тивності: для довільних, , називається напівгрупою.

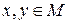Означення 6. Напівгрупа A =, в якій операція f задовольняє закону комутативності: для довільних, , називається комутативною або абелевою.

Означення 7. Напівгрупа A =, в якій кожний елемент має оберне­ний, тобто для довільного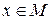, знайдеться у такий, що 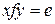називається группою (елемент у називається оберненим до елемента х і позначається так: ).

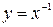Означення 8. Алгебра A =називається дистрибутивною, якщо операції для довільних задовольняють законам дистрибутивності:

1) 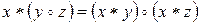; 2) .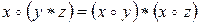

Означення 9. В алгебрі A =два елементи т_а та т_b називаються такими, що доповнюють друг друга, якщо: 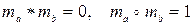.Елемент m_b позначають і називають доповненням елемента т_а в алгебрі A. При чому для довільного 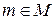виконується закон подвійного доповнення .

Означення 10. Алгебра A =називається алгеброю з доповненням, якщо вона має структурний нуль і для кожного 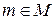існує його доповнення . Крім того для довільних виконуються закони де Моргана, .

Означення 11. Алгебра A =називається кільцем, якщо в алгебрі виконується перший закон дистрибутивності, відносно операції утворює абелеву групу, а відносно операції * - абелеву напівтрупу.

Означення 12. Кільце A =, в якому елементи відмінні від нуля утворюють групу відносно операції * - називається тілом, а якщо ця група комутативна, то - полем.

Розглянемо приклади.

1. A =á N, +ñ - абелева напівгрупа без нуля.

2. A =á N,×ñ - абелева напівгрупа з одиницею.

3. A =á Z, +,×ñ - кільце цілих чисел.

4. A =á Q, +,×ñ - поле раціональних чисел.

5. A =á R, +,×ñ - поле дійсних чисел.

6. A =á P (x), +,×ñ - кільце поліномів (P (x) – множина поліномів довільного степеня).

7. A=á,*ñ, де - множина підстановок. Нехай 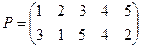, 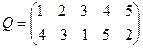дві підстановки. Послідовна дія цих підстановок називається їхнім добутком.

Відносно цієї операції множина підстановок утворює групу. Дійсно:

а) ;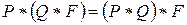

б) (Е – одинична підстановка);

в) якщо Р та Q такі, що , то Q називається оберненою до підстановки Р. При чому для довільної підстановки завжди існує обернена, щоб її визначити, необхідно переставити місцями верхній та нижній рядки. Добавить примеров

Означення 13. Алгебра A = , що відносно кожної операції є ідемпотентною абелевою напівгрупою, називається структурою, якщо операції підкоряються закону поглинання 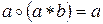, для довільних .

Означення 14. Якщо структуру побудовано на алгебрі, що є дистрибутивною і має доповнення, то вона називається булевою алгеброю і позначається A =.

Відмітимо, що окрім перерахованих законів, яким підкоряються операції булевої алгебри, мають місце й інші, серед яких виділимо такі:

а) закони склеювання: , ;

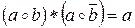б) закони Порецького: , .

Дата добавления: 2014-01-15