Лекция № 11. по учебной дисциплине

ЛЕКЦИЯ

по учебной дисциплине

«Теоретическая механика»

Раздел II. «Кинематика»

Тема № 2.2. «Кинематика точки»

«Ускорение точки»

Минск-2010г.

УЧЕБНЫЕ И ВОСПИТАТЕЛЬНЫЕ ЦЕЛИ:

1. Ознакомиться с ускорением точки при различных способах задания движения.

2. Изучить касательное и нормальное ускорения точки.

3. Воспитание у обучаемых общей и технической культуры, чувства гордости за выбранную воинскую профессию.

УЧЕБНЫЕ ВОПРОСЫ:

1. Ускорение точки при различных способах задания движения.Естественные координатные оси. Вектор кривизны.

2. Определение ускорения точки при естественном способе задания движения. Касательное и нормальное ускорения точки.

3. Некоторые частные случаи движения точки.

ВРЕМЯ: два академических часа

МЕСТО: учебная аудитория

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПРЕПОДАВАТЕЛЮ:

Изложение материала проводится в сочетании дедуктивного (от общего к частному – определения, анализ формул и т.п.) и индуктивного (от частного к общему – вывод формул, примеры работы механизмов и т.п.) методов. Рассматриваемые вопросы иллюстрируются плакатами и макетами механических устройств.

Активизация работы обучаемых достигается проблемным изложением материала, путём постановки и решения проблемных вопросов и задач, а также использование продуктивных методов обучения: частично-поискового и исследовательского.

Воспитательные цели достигаются личным примером преподавателя, требовательностью в выполнении руководящих документов и проведением информационной работы в идеологической и научно-технической области.

УЧЕБНО-МАТЕРИАЛЬНОЕ ОБЕСПЕЧЕНИЕ: плакаты.

УЧЕБНАЯ ЛИТЕРАТУРА:

1. Курс теоретической механики / Под ред. К.С. Колесникова. М: Изд-во МГТУ им. Н.Э. Баумана, 2000 г.

2. Никитин Н.Н. Курс теоретической механики: Учебник. – М.: Изд-во Высшая школа, 1990 г. 600 стр.

3. Яблонский А.А., Никифорова В.М. Курс теоретической механики. Статика. Кинематика. Динамика. – М.: Интеграл-ПРЕСС, 2006.

4. Тульев В.Д. Теоретическая механика. Статика и кинематика. – Мн.: Книжный дом, 2004.

5. Хижняк Е.И. Теоретическая механика. Методические рекомендации курсантам по подготовке к занятиям. Ч.III. – Мн.: ВА РБ, 2006.

ПЛАН ЛЕКЦИИ:

I. ВСТУПИТЕЛЬНАЯ ЧАСТЬ (3 минуты):

Проверка наличия обучаемых, внешнего вида и их готовность к занятию (наличие конспектов и чертежных принадлежностей).

Объявление темы, учебных вопросов и целей занятия, практической значимости тематики нового материала в изучении дисциплин по профилю обучения.

II. ОСНОВНАЯ ЧАСТЬ (85 минут):

Вопрос 1. Ускорение точки при различных способах задания движения.

Ускорение точки можно задать тремя способами:

1. векторный;

2. координатный;

3. естественный.

Векторный способ задания движения.

Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.

Пусть в некоторый момент времени t движущаяся точка находится в положении М и движется со скорость 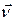, а в момент t₁ находится в положение M₁ и имеет скорость 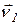(рис. 1).

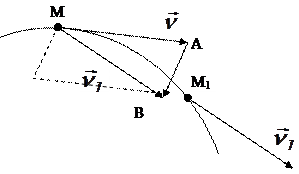Рисунок 1

Тогда за промежуток времени 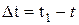скорость точки получает приращение 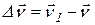. Для построения вектора 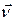отложим от точки М вектор, равный 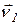, и построим параллелограмм, в котором диагональю будет 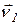, а одной из сторон 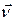. Тогда, очевидно, вторая сторона и будет изображать вектор 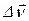. Заметим, что вектор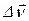всегда направлен в сторону вогнутости траектории.

Отношение приращения вектора скорости 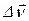к соответствующему промежутку времени 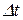определяет вектор среднего ускорения точки за этот промежуток времени:

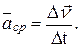(1)

Вектор среднего ускорения имеет, очевидно, то же направление, что и вектор 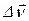, т. е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени t называетсявекторная величина 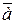, к которой стремится среднее ускорение 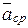при стремлении промежутка времени Δt к нулю:

,

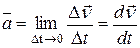или, с учетом определения скорости из предыдущей лекции

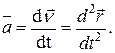(2)

Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.

Размерность ускорения - длина/(время)²; в качестве единицы измерения применяется обычно м/сек².

Из формулы (2) следует также, что вектор ускорения точки 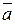равен отношению элементарного приращения вектора скорости 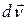к соответствующему промежутку времени dt.

Найдем, как располагается вектор 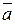по отношению к траектории точки При прямолинейном движении вектор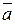направлен, очевидно, вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения 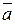, так же как и вектор 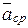, лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор 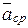будет направлен в сторону вогнутости траектории и будет лежать в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке M₁. В пределе, когда точка M₁ стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости. Следовательно, в общем случае вектор ускорения 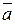лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Ускорения точки при координатном способе задания движения.

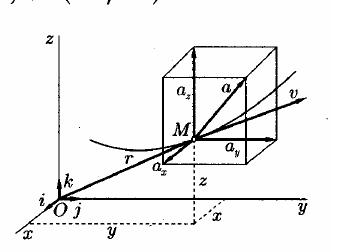
Рисунок 2

Вектор ускорения точки 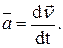Отсюда на основании теоремы о проекции производной получаем:

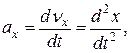
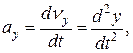
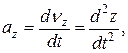(3)

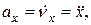
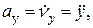
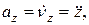или (4)

т.е. проекции ускорения точки на оси координат равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул:

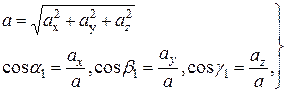(5)

где α₁, β₁, γ₁ – углы, образуемые вектором ускорения с осями координат.

В случае же прямолинейного движения, которое задается одним уравнением x=f(t), будем иметь

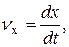
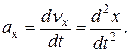(6)

Так как проекции на другие оси отсутствуют, то, следовательно, в данном случае 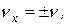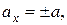т. е. при прямолинейном движении формулы (9) непосредственно определяют скорость и ускорение точки.

Дата добавления: 2014-01-15