Проецирующие прямые

Прямые перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим.

3.2.1 Горизонтально проецирующая прямая это прямая, перпендикулярная П₁ (рис. 2.6).

Точки M и N называются КОНКУРИРУЮЩИМИ. Видимой является точка M, т.к. она встречается первой по направлению проецирования.

Рис. 2.6

Горизонтальная проекция этой прямой вырождается в точку, а фронтальная проекция (А₂В₂) перпендикулярна координатной оси x₁₂. Горизонтально проецирующая прямая параллельна одновременно П₂ и П₃, следовательно на них она проецируется без искажения (в натуральную величину НВ

| А₂В₂ | = | А₃В₃ | = |АВ|).

3.2.2. Фронтально проецирующая прямая перпендикулярна плоскости П₂ (риc.2.7).

Рис. 2.7

Фронтальная проекция этой прямой вырождается в точку, а горизонтальная проекция (С₁D₁) перпендикулярна координатной оси x₁₂. Фронтально проецирующая прямая параллельна одновременно П₁ и П₃ и проецируется на них без искажения (в натуральную величину НВ).

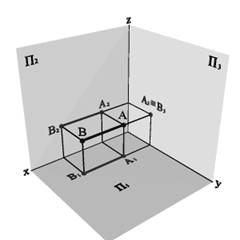
3.2.3. Профильно проецирующая прямая перпендикулярная плоскости П₃

(рис. 2.8).

Рис. 2.8

Профильная проекция этой прямой вырождается в точку, а горизонтальная и фронтальная проекции перпендикулярны координатным осям y и z. Профильно проецирующая прямая параллельна одновременно П₁ и П₂ и проецируется на них в натуральную величину.

Очевидно, что проецирующие прямые представляют собой частный случай прямых уровня.

Точки, принадлежащие одной и той же проецирующей прямой, называются конкурирующими относительно плоскости проекций, которой перпендикулярна данная прямая.

Конкурирующие точки применяются для решения вопроса видимости проекций геометрических фигур на комплексных чертежах.

4 ПРОЕЦИРОВАНИЕ ПРЯМОЙ НА ДОПОЛНИТЕЛЬНЫЕ

ПЛОСКОСТИ ПРОЕКЦИЙ

Проецирование отрезка прямой общего положения на дополнительные плоскости проекций сводится к получению на них проекций, занимающих частные положения.

На дополнительную плоскость Π₄ отрезок | A B | проецируется в натуральную величину, а на плоскости Π₅ вырождается в точку (рис. 2.9).

Рис. 2.9

5 НАТУРАЛЬНАЯ ВЕЛИЧИНА ОТРЕЗКА

Натуральная величина отрезка общего положения может быть найдена на комплексном чертеже как гипотенуза прямоугольного треугольника. Если взять как катет одну из проекций отрезка, а второй катет построить равным разности координат концов отрезка до той же плоскости проекций, на которой взят первый катет. Гипотенуза такого треугольника будет натуральной величиной отрезка общего положения (рис. 2.10).

Рис. 2.10

6 ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ

Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися (рис. 2.11).

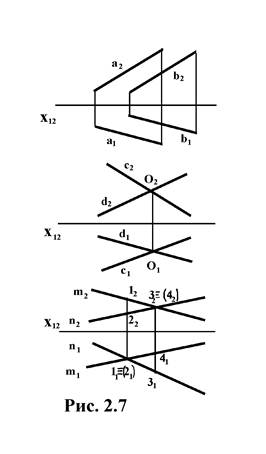Рис. 2.11

Дата добавления: 2014-01-15