Дифференциальное уравнение с двумя неизвестными переменными

Классификация уравнений с частными производными второго порядка

Определение 1. Уравнением в частных производных второго порядка с двумя неизвестными переменными x, y называется соотношением между неизвестной функцией 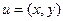и ее частными производными до второго порядка включительно:

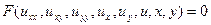(1)

Определение 2. Уравнение называется линейнымотносительно старших производных, если оно имеет вид

(2)

Где – коэффициенты, зависящие от x y. Если зависят не только от x и y, но и от 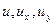, то уравнение называется квазилинейным.

Определение 3. Уравнение называется линейным, если оно линейно как относительно старших производных, так и относительно самой функции 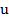и её производных :

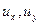(3)

Где 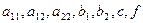–функции, зависящие только от . Если данные величины не зависят от x и y, то уравнение называется уравнением с постоянными коэффициентами.

Определение 4. Уравнение (3) называется однородным, если

Поставим задачу. С помощью преобразований переменных вводим новые переменные, которые допускают обратные преобразования:

(4)

Переменные 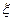и должны быть дважды непрерывно дифференцируемыми функциями, причем Якобиан преобразований:

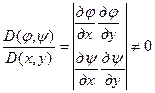
В этой области, которую мы рассматриваем.

Это условие означает что переменные 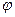и независимы и возможны обратные преобразования.

При преобразовании переменных 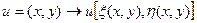в новых переменных уравнение (3) перепишется следующем в виде:

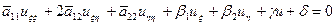(5)

где

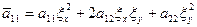
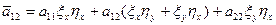
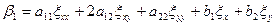
Функция должна быть дважды дифференцируема. Это значит что смешанные производные будут одинаковы.

Уравнение (5) эквивалентно (3) только записано в новых переменных.

Можно показать что .

Где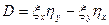

Новые переменные можно выбрать таки образом, что выполняется одно из 3 условий:

1.

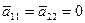
2.

3. ;

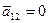Выбор новых переменных. Переменные 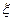и выбираем таким образом, чтобы коэффициент 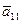был равен нулю. Рассмотрим уравнение с частными производными 1-ого порядка

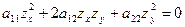(6)

Пусть 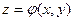– частное решение данного уравнения. Если положить, то .

Таки образом, задача о рациональном выборе новых переменных связана с решением уравнения(6).

Лемма 1. Если 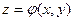является частным решением уравнения (6), то соотношение 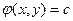представляет собой общий интеграл обыкновенного дифференциального уравнения

(7)

Лемма 2.(обратная лемме 1) Если 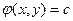представляет собой общий интеграл обыкновенного дифференциального уравнения

То функция 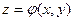удовлетворяет уравнению (6).

Уравнение (7) называют характеристическим для уравнения (2), а его интегралы – характеристиками.

Таким образом, леммы дают алгоритм, которому надо следовать при упрощении уравнений. Если положить и 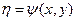,то получим два общих интеграла.

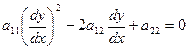
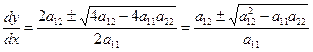(8)

Знак определяет тип уравнения (2).

Определение 5. Уравнение (2) в точке М называется уравнением:

гиперболического типа, если ,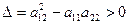

параболического типа, если ,

эллиптического типа, если .

Дата добавления: 2014-01-15