Поперечные колебания струны закрепленной на концах

Граничные и начальные условия

При математическом описании физического процесса надо поставить задачу, т.е. сформулировать условия достаточные для однозначного определения процесса. Дифференциальные уравнения с частыми производными имеет множество решений. Поэтому когда физическая задача сводится к частным производным для однородного решения задачи необходимо присоединить некоторые дополнительные условия. В случае ОДУ второго порядка, решение может быть определено однозначно.

Задача 1.

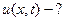
Условие жесткого закрепления струны в точках 0 и: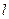

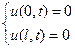(1)

Процесс колебания струны зависит и от начального числа скоростей.

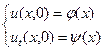(2)

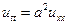(3)

Если концы струны движутся по заданному закону, то граничные условия примет вид:

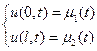(4)

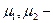заданные функции времени.

Задача 2. Продольные колебания.

Возьмем пружину, у которой один конец закреплен на подвесе, второй не закреплен, тогда:

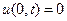
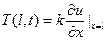(5)

Если на свободном конце неподвижный груз, то уравнение будет иметь вид:

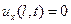(6)

Это условие свободного конца

Задача 3.

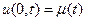
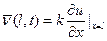(7)

Задача 4.

Граничные условия упругого закрепления в точке .

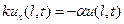
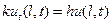(8)

Где

где 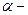коэффициент жесткости закрепления.

Конец может перемещаться, но упругая сила закрепления вызывает на этом конце натяжение, стремящееся вернуть в исходное положении. Эта сила, согласно закону Гука, пропорциональна смещению.

Задача 5.

Если точка относительно которой имеет место упругое закрепление перемещается и ее отклонение от начального положения задается функцией :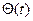

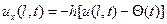(9)

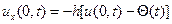(10)

Рассмотрим случай жесткого закрепления 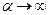тогда .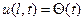

Условие мягкого закрепления это значит что большие сдвиги вызывают малые натяжения. И тогда получаем условие 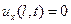, а это есть условие свободного конца.

Мы будем рассматривать три типа граничных условий:

1. граничное условие первого рода

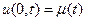- заданный режим

2. граничное условие второго рода

- заданная сила

3. граничное условие третьего рода

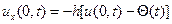- условие упругого закрепления

Если 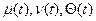равны нулю, то эти условия называются однородными. Комбинируя различные типы уравнений, получаем шесть типов краевых задач.

Сформулируем первую (простейшую) краевую задачу. Найти функцию 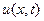определенную в области 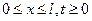, удовлетворяет уравнению:

, .

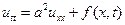Граничные условия: , .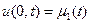

Начальные условия: , , .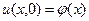

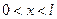Влияние граничных условий в точке 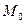достаточно удаленной от границы складывается через достаточно большой промежуток времени. Если нас интерес промежуток времени, где влияние границ несущественно, то вместо полной задачи можно рассмотреть:

1. Для неограниченной струны, где начальные условия не нужны.

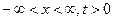
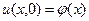, - это предельный случай (задача Коши).

2.

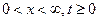
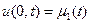- это задача о полу бесконечной струне, начальные условия несущественны.

Для уравнения с частными производными второго порядка существует несколько методов:

1. Метод распространения вол (метод Даламбера).

2. Метод функции Грина.

3. Метод разделения переменных (метод Фурье).

Дата добавления: 2014-01-15