Интерпретация решения

Метод разделения переменных (метод Фурье)

Метод разделения переменных или метод Фурье является одним из самых распространенных методов решения уравнений с частными производными. Этот метод можно применить для решения уравнения гиперболического, параболического и эллиптического типов.

Задача. Найти решение уравнения

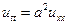(1)

Где

Однородные граничные условия:

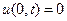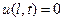, (2)

Начальные условия:

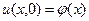, (3)

В силу линейности и однородности уравнение (1) сумма частных решений также является решением этого уравнения. Если мы будем располагать достаточно большим числом частных решений, то путем их суммирования можно найти искомое решение.

Поставим вспомогательную задачу. Найти решение уравнения (1) тождественно не равного нулю, удовлетворяющее условию(2) решение которого можно представить виде:

(4)

Предполагаемую форму решения (4) подставляем в (1) и поделим на 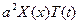, получаем:

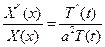(5)

Такое равенство возможно, если прировнять к const.

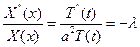
Из данного соотношения получаем ОДУ для нахождения функций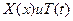

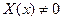(6)

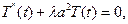
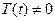(7)

Граничные условия (2) дают

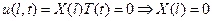
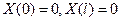(8)

(8) – дополнительное условие для 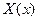. Для функции 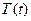дополнительных условий нет.

При решении уравнений (6) с условиями (8) мы приходим к простейшей задаче о собственных значениях и собственных функциях.

Найдем те значения параметра 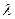, при которых существует нетривиальные решения задачи (6) с условиями (8), а также найти эти решения. Таки значения параметра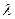называются собственными значениями, а соответствующее им нетривиальное решение – собственные значения функции задачи (6).

1.

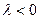
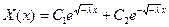
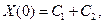
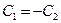
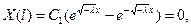
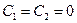
2.

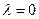
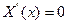
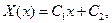
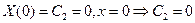
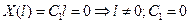
1 и 2 – это тривиальный случай.

3. Нетривиальное решение будет существовать только при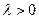

В этом случае общее решение можно записать виде:

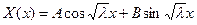
Граничные условия дают:

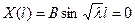
Так как мы ищем решения, не равные тождественно нулю, то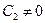, поэтому 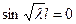или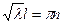

Следовательно, нетривиальное решение задачи возможны лишь при значениях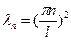

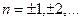
Этим собственным значением соответствуют собственные функции

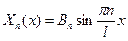(10)

Где 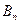– произвольная постоянна. Или с точностью до произвольного постоянного множителя:

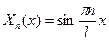
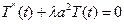
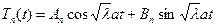(11)

Значениям 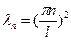соответствуют решение уравнения (7):

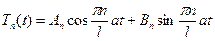(12)

Таки образом, частное решение (1) имеет вид

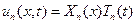
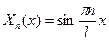
Общее решение записывается как сумма частных

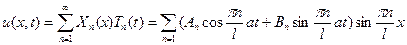(13)

Где 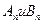– коэффициенты, которые еще не определены.

Это решение автоматически удовлетворяет граничным условиям, а начальные условия позволяют определить .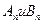

Начальные условия:

(14)

(15)

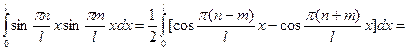
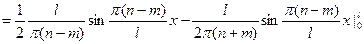
Рассмотрим случай когда.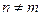

При подстановке верхнего и нижнего предела даст ноль, следовательно доказали ортогональность решения.

Рассмотрим случай когда .

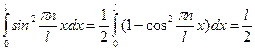
Результатом интегрирования будет:

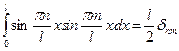(16)

Введем функцию нормированную на единицу. Если мы до множим на 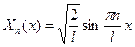, получим .

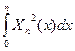Вернемся к формулам (14) и (15).

Данное выражение умножаем на и интегрируем:

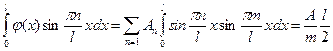
По формуле (16) заменяем вторую часть уравнения на 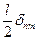. В итоге получаем, что данное выражение равно.

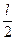Выражение для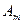будет иметь вид:

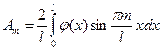
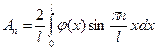(17)

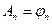
Аналогично для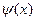

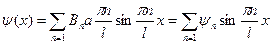
Коэффициенты определены, задача решена.

Функцию можно представить в виде:

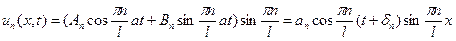(18)

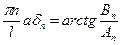(19)

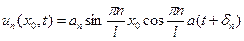
Каждая точка совершает гармоническое колебание. Амплитуда колебания зависит от х, следовательно, для каждой точке 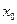своя амплитуда колебания, равная: 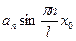. такое движение струны называется стоячей волной.

,

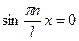
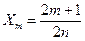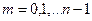
Точка в которой достигается максимум значения 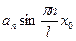это кучность стоячей волны.

Профиль стоячей волны в любой момент времени:

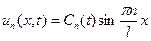
Где

(20)

В этот момент времени когда 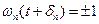, т.е. отклонение достигается максимальной амплитудой .

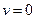Для малых поперечных волн струны

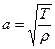
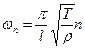
Энергия n –ой стоячей волны:

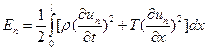
Берем формулу частных решений и дифференцируем её:

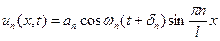
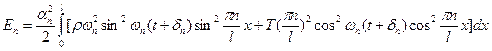
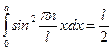
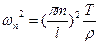
Энергия n – ой гармоники зависит от способа возбуждения колебания. Колебания струны воспринимается по звуку издаваемой струной. Докажем, что звук струны является тоном (простой тон – это какая то конкретная частота). Общее решение, с математической точки зрения, это стоячая волна. Разложение звука на простые тоны подтверждают эксперимент. Высокая нота зависит от частоты колебания, сила тона определяется его энергией, следовательно, его амплитуды. Самый низкий тон, который может издавать струна, самая низкая собственная частота 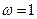называется основной тон. Остальные тона будут кратными 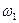и эти частоты называются обертонами. Тембр звука – зависит от присутствия наряду с основным тоном и как распределение энергии по этим гармоникам. Низкий тон струны и ее тембр зависит от способа возбуждения колебания, который в свою очередь зависит от начальных условий:

,

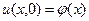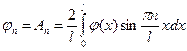
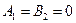, то тогда низкий тон не будет 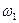, тогда нижней частотой будет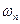, где .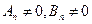

Обычно струна издает один и тот же тон. Приведем струну в колебания, оттягивая ее в одну сторону:

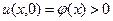
Тогда выражение для коэффициента 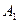будет иметь вид:

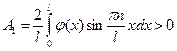
а следовательно коэффициент будет значительно меньше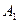

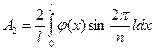
При 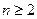функция синус является знакопеременной.

Колебание струны.

Если начальная функция нечетная относительно середины отрезка, тогда 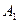будет нулевым, а нижним тоном будет являться частота

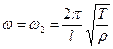
Если в звучащей струне прикоснутся точно в середине, то ее звук резко изменится, и она звучит в октаву своего тона – флажолет.

Дата добавления: 2014-01-15