По данным выборки

Оценка точности вычисления генеральной средней

Совокупности по данным выборки.

Оценка точности вычисления параметров генеральной

Обозначим точность приближенного равенства 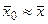буквой ε. Тогда определение точности вычисления генеральной средней по данным выборки сведется к определению вероятности α, т. е. вероятности того, что истинное значение 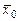находится в пределах , где ε > 0, т. е.

.

Для определения вероятности а пользуются распределением величины t:

. (4)

Если генеральная совокупность имеет нормальное распределение, то величина t при любом п следует закону распределения Стьюдента, который имеет следующее выражение:

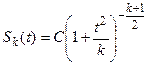, (5)

где S_k (t) — дифференциальная функция распределения t;

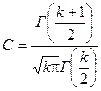— постоянный множитель, зависящий только от числа степеней свободы k = п — 1. Символом Г(k) здесь обозначена гамма-функция (интеграл Эйлера):

.

Из выражения (5) следует, что распределение Стьюдента зависит только от переменной t и параметра k = п — 1. Поэтому когда задана вероятность α, то можно найти такое положительное число t _α которое будет зависеть только от α и n по равенству

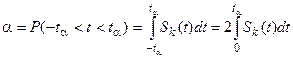. (6)

Учитывая, что , левую часть этого равенства можно преобразовать так:

.

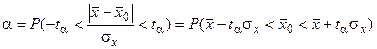Следовательно,

(7)

Полагая t _ασ _x = ε, получим

.

Таблица значений t _α определяемых этим равенством, приведена в приложении 1 (см. в конце лекции). При помощи этой таблицы можно определить одно из трех значений: вероятность α, точность ε или объем выборки п, задаваясь предварительно значениями каких-либо двух из этих величин.

Пример 1. По выборке объема n = 15 найдено 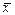= 20,4 и s = 0,8. Определить истинное значение генеральной средней.

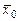Генеральная средняя 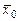определяется доверительными границами

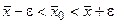, где .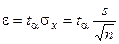

Зададимся надежностью α = 0,98. Тогда по таблице приложения 1 при k = п - 1 = 14 находим t_а = 2,62. Поэтому

.

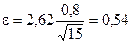Следовательно,

(20,4—0,54) <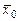< (20,4+0,54), т. е. 19,86 <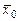< 20,94.

Пример 2. Установить, какой объем n выборки необходимо взять, чтобы определить по этой выборке генеральную среднюю с точностью и вероятностью α = 0,95.

Так как , то, следовательно, t _α = 2. По таблице приложения 1 для α = 0,95 находим значение t _α= 2, которому соответствует k = 60. Но k = п - 1, следовательно, п == 61.

Все изложенное об оценке точности и вероятности вычисления генеральной средней по выборочной средней является справедливым только для случаев, когда выборки берутся из генеральной совокупности, имеющей нормальное распределение случайной величины х или когда распределение х в генеральной совокупности не очень сильно отличается от нормального. Если же распределение х в генеральной совокупности сильно отличается от нормального, то в этом случае вероятность α и точность ε приближенного равенства 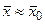можно определить только для больших выборок с помощью формул (9) и (10), но полученные значения α и ε не будут точными, а будут носить лишь приближенный характер.

Дата добавления: 2014-01-15