Отклонения генеральной совокупности по данным выборки

Оценка точности вычисления среднего квадратического

На практике иногда необходимо найти неизвестное среднее квад-ратическое отклонение генеральной совокупности σ₀ по среднему квадратическому отклонению s малой выборки, когда ее объем n < 25. Для малых выборок s вычисляется по формуле

,

где в отличие от формулы (11), приведенной в лекции 1, в знаменателе берется (п — 1), для того чтобы компенсировать систематическую ошибку, возникающую при оценке σ₀ по s при малом числе n.

Эта задача сводится к определению вероятности α приближенного равенства , точность которого равна ε:

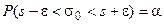. (13)

Если известно, что случайная величина х в генеральной совокупности подчинена нормальному закону распределения, то величина

имеет распределение, которое носит название -распределения. Дифференциальная функция этого распределения или плотность вероятности величины имеет выражение

при χ > 0.

При помощи этой функции -распределения можно вычислить и вероятность α:

.

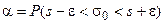Для этой цели, полагая, что s - ε > 0, преобразуем находящееся в скобках неравенство следующим образом:

.

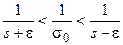Умножим полученное неравенство на положительное число

.

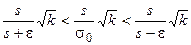Обозначив и , получим

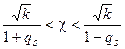или .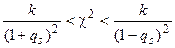

Вероятность этого неравенства равна интегралу

. (14)

Но левая часть этого уравнения есть преобразованное выражение вероятности

.

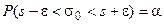Следовательно, можно написать

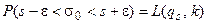(15)

или

. ( 16 )

Значения интеграла L (q_s, k)приведены в таблице приложения 2.

Таким образом, по таблице приложения 2 можно определить вероятность α, т. е. вероятность того, что отклонения σ₀ от s не превосходят ε = q_ss.

Необходимо заметить, что если s < ε, то исходное неравенство для σ₀

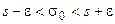
надо заменить неравенством

,

так как величина σ₀ должна быть положительной. В этом случае неравенство для χ примет вид

и вероятность его будет определяться интегралом

.

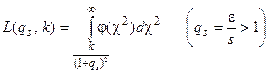Значения этого интеграла также приведены в приложении 2. При помощи таблицы значений вероятностей L (q_s, k) (см. приложение 2) можно решать задачи трех типов:

1) по заданной точности ε = q_ss и объеме выборки n определить вероятность α приближенного равенства ;

2) по заданной вероятности α приближенного равенства и объеме выборки п определить точность ε = q_ss этого равенства;

3) по заданной точности ε и вероятности α приближенного равенства определить необходимый объем n выборки.

Пример 4. По выборке объема п = 15 вычислено среднее квадратическое отклонение n = 0,6. Определить вероятность α приближенного равенства при точности ε = 0,12. По таблице приложения 2 для

k = n - 1 = 15 - 1 = 14 и

находим

α = 0,701;

P (0,6—0,12 < σ₀ < 0,6 + 0,12) = 0,701;

P (0,48 < σ₀ < 0,72) = 0,701.

Пример 5. Определить точность ε приближенного равенства с вероятностью α = 0,96, если п = 15 и s = 0,12. По таблице приложения 2 находим для k = 15 - 1 = 14 и α = 0,96 q_s = 0,5.

Следовательно,

ε = q_ss = 0,5 0,12= 0,06;

σ₀ = s ± ε = 0,12±0,06

или

0,06 < σ₀ < 0,18.

Пример 6. Определить n, при котором s будет отличаться от σ₀ на ±0,2 с вероятностью α = 0,96:

ε = q_ss = 0,2 s; q_s = 0,2.

По таблице приложения 2 при (q_s ⁼ 0,2 и α = 0,96 находим k = 60. Но k = = n — 1, следовательно,

n = k +1 = 60+1 = 61.

Рассмотренная методика оценки приближенного равенства действительна для того случая, когда случайная величина х распределена в генеральной совокупности по нормальному закону. Если же распределение х в генеральной совокупности отличается от нормального, то определение неизвестного его среднего квадратического отклонения возможно более или менее точно в большинстве случаев только при большом числе наблюдений. Именно, в этом случае можно с большой вероятностью полагать, что среднее квадратическое отклонение генеральной совокупности σ₀ отличается от выборочного s не более чем на .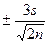

ПРИЛОЖЕНИЕ 1

Таблица значений , для которых вероятность

k	вероятность a
0,9	0,95	0,98	0,99	0,999
	6,31	12,71	31,82	63,66	636,2
	2,02	4,30	6,97	9,93	31,60
	2,35	3,18	4,54	5,84	12,94
	2,13	2,78	3,75	4,60	8,61
	2,02	2,57	3,37	4,03	6,86
	1,94	2,45	3,14	3,70	5,96
	1,90	2,37	3,00	3,50	5,40
	1,86	2,30	2,90	3,36	5,04
	1,83	2,26	2,82	3,25	4,78
	1,81	2,23	2,76	3,17	4,59
	1,80	2,20	2,72	3,11	4,49
	1,78	2,18	2,68	3,06	4,32
	1,77	2,16	2,65	3,01	4,22
	1,76	2,14	2,62	2,98	4,14
	1,75	2,13	2,60	2,95	4,07
	1,75	2,12	2,58	3,92	4,02
	1,74	2,11	2,57	2,90	3,97
	1,73	2,10	2,55	2,88	3,92
	1,73	2,09	2,54	2,86	3,88
	1,72	2,09	2,53	2,85	3,85
	1,72	2,08	2,52	2,83	3,82
	1,72	2,07	2,51	2,82	3,79
	1,71	2,07	2,50	2,81	3,77
	1,71	2,06	2,49	2,80	3,75
	1,71	2,06	2,49	2,79	3,72
	1,71	2,06	2,48	2,78	3,71
	1,70	2,05	2,47	2,77	3,69
	1,70	2,05	2,47	2,76	3,67
	1,70	2,05	2,46	2,76	3,66
	1,70	2,04	2,46	2,45	3,65
	1,68	2,02	2,42	2,70	3,55
	1,67	2,00	2,39	2,66	6,46
	1,66	1,98	2,36	2,62	3,37
	1,65	1,96	2,33	2,58	3,29

ПРИЛОЖЕНИЕ 2

Таблица вероятностей

k
0,10	0,15	0,20	0,25	0,30	0,40	0,50	0.60	0,70	0,80	0,90	1,00	1,25	1,50	1,75	2,00	2,50	3,00
	0,264	0 388	0,501	0,599	0,681	0,791	0,849	0,886	0,913	0,933	0,948	0,959	0,978	0,987	0,992	0,995	0,998	0,999
																	1,000	1,000
																1,000	—	—
														1,000	1,000	—	—	—
														—	—	—	—	—
													1,000	—	—	—	—	—
													—	—	—	—	—	—
												1,000	—	—	—	—	—	—
										1,000	1,000	—	—	—	—	—	—	—
									1,000	—	—	—	—	—	—	—	—	—
									—	—	—	—	—	—	—	—	—	—
								1,000	—	—	—	—	—	—	—	—	—	—
								—	—	—	—	—	—	—	—	—	—	—
								—	—	—	—	—	—	—	—	—	—	—
							1,000	—	—	—	—	—	—	—	—	—	—	—
						1,000	—	—	—	—	—	—	—	—	—	—	—	—
						—	—	—	—	—	—	—	—	—	—	—	—	—
						—	—	—	—	—	—	—	—	—	—	—	—	—
					1,000	—	—	—	—	—	—	—	—	—	—	—	—	—
				1,000	—	—	—	—	—	—	—	—	—	—	—	—	—	—
			1,000	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—
			1,000	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—
		1,000	1,000	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—
	1,000	1,000	1,000	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—

Дата добавления: 2014-01-15