
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Числовые характеристики СВ
|
|
|
|
Пр.3.
Случайные величины
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые сначала не могут быть учтены.
Пример 1. Число родившихся детей в городе в течение суток – СВ, которая принимает значения 1, 2, 3, …
Пример 2. Прибыль фирмы – СВ. Возможные значения этой величины принадлежат некоторому промежутку.
Будем обозначать случайные величины прописными буквами X, Y, Z …, а их возможные значения соответствующими строчными буквами x, y, z …
Различают следующие виды случайных величин:
Дискретная (прерывная) СВ – величина, которая принимает отдельные, изолированные числовые значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. (Пр.1)
Непрерывная случайная величина – СВ, которая может принимать любые числовые значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной СВ бесконечно. (Пр. 2).
Для задания дискретной СВ недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.
Законом распределения дискретной СВ называют соответствие между возможными значениями этой величины и их вероятностями. Закон распределения можно задать таблично, аналитически и графически.
При табличном задании первая строка таблицы содержит возможные значения, а вторая – их вероятности:
| Х | х 1 | х 2 | … | хn |
| р | р 1 | р 2 | … | рn |
Т.к. в одном испытании случайная величина принимает одно и только одно возможное значение, то события Х = х 1, Х = х 2,…, Х = хn образуют полную группу. => Сумма вероятностей этих событий равна 1: р 1 + р 2 + … + рn = 1.
Если множество возможных значений Х бесконечно (счетно), то ряд р 1 + р 2 + … сходится, и его сумма равна 1.
Пример 3. В денежной лотерее выпущено 100 билетов. Разыгрывается 1 выигрыш в 50 рублей и 10 выигрышей по 5 руб. Найти закон распределения СВ Х – стоимости возможного выигрыша владельца лотерейного билета.
Решение. Х – дискретная СВ. Ее возможные значения: х 1 = 0, х 2 = 5, х 3 = 50. Вероятности этих значений: р 1 = 0,89, р 2 = 0,1, р 3 = 0,01. (проверка: 0,89 + 0,1 + 0,01 = 1)
Тогда закон распределения:
| Х | |||
| р | 0,89 | 0,1 | 0,01 |
Для наглядности закон распределения дискретной СВ можно изобразить и графически, для чего в прямоугольной системе координат строят точки (xi, pi), а затем соединяют их отрезками. Полученная ломанная называется многоугольником или полигоном распределения.
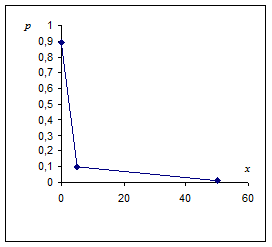
Аналитически СВ задается либо функцией распределения, либо плотностью вероятностей.
Функцией распределения СВ Х называют функцию 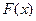 , определяющую вероятность того, что СВ Х принимает значение, меньшее, чем х:
, определяющую вероятность того, что СВ Х принимает значение, меньшее, чем х:  .
.
Иногда эту функцию называют функцией накопленной вероятности или кумулятивной функцией распределения.
Свойства функции распределения:
1. 0 ≤ 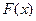 ≤ 1.
≤ 1.
2. 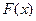 - неубывающая функция, т.е.
- неубывающая функция, т.е. 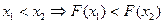 .
.
3. 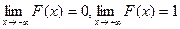 .
.
4. 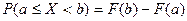 .
.
5. 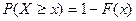 .
.
6. Если возможные значения СВ Х принадлежат отрезку [a, b], то 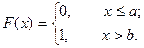
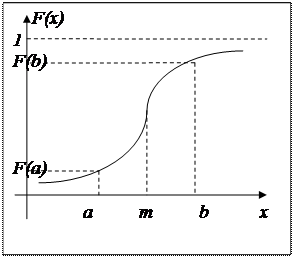
График функции распределения даёт наглядное представление о вероятности изменения значений СВ.
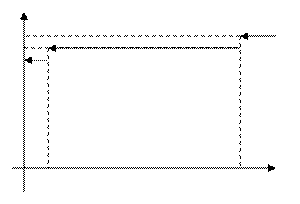
Для примера 3 функция распределения и её график имеют вид:
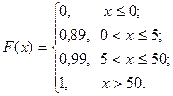
| 
|
Для непрерывной СВ нельзя определить вероятность того, что она принимает некоторое конкретное значение, а следовательно непрерывную СВ нельзя задать таблично. Поэтому для описания непрерывной СВ может быть использована функция распределения. При этом она является непрерывной неубывающей функцией, изменяющейся от 0 до 1.
Плотностью вероятности (плотностью распределения вероятностей) непрерывной СВ Х называют функцию 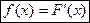 .
.
Свойства плотности вероятности:
1. 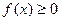 . 2.
. 2. 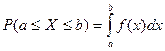 .
.
3. 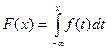 . 4.
. 4. 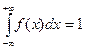 .
.
Для непрерывной СВ справедливы равенства:
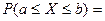
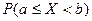 =
=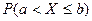 =
=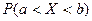 .
.
| 
|
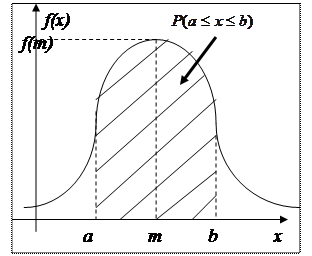
Площадь под графиком кривой плотности вероятности равна единице.
Площадь заштрихованной области на рисунке равна: 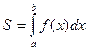 =
=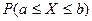 .
.
Вероятность попадания значений СВ в «хвосты» распределения, т.е. в интервалы  и
и 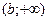 , равна 1 –
, равна 1 – 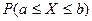 . Т.о. с помощью плотности вероятности можно определить вероятность попадания непрерывной СВ Х в заданный интервал
. Т.о. с помощью плотности вероятности можно определить вероятность попадания непрерывной СВ Х в заданный интервал 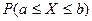 , что имеет большое прикладное значение.
, что имеет большое прикладное значение.
Числовыми характеристиками СВ называют числа, которые описывают СВ суммарно. К таким числовым характеристикам относится математическое ожидание. Оно характеризует среднее ожидаемое значение СВ, т.е. приблизительно равно его среднему значению. Для решения многих задач достаточно знать МО (например, при оценивании покупательной способности населения достаточно знать средний доход).
Математическим ожиданием дискретной СВ называют сумму произведений всех возможных ее значений на их вероятности.
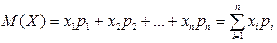 .
.
Если дискретная СВ принимает счетное множество всевозможных значений, то
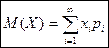
Причем мат.ожидание существует, если ряд в правой части сходится абсолютно.
Для непрерывной СВ: M(X) =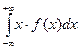 .
.
Замечание. Мат.ожидание – неслучайная постоянная величина.
Пример 4. Найти мат.ожидание дискретной СВ Х, зная закон ее распределения:
| Х | |||
| р | 0,1 | 0,6 | 0,3 |
Решение. Искомое мат.ожидание М (Х) = 3∙0,1 + 5∙0,6 + 2∙0,3 = 3,9.
Мат.ожидание числа появления события в одном испытании равно вероятности этого события.
Мат.ожидание приближенно равно (тем больше, чем больше число испытаний) среднему арифметическому наблюдаемых значений СВ.
Замечание. МО больше наименьшего и меньше наибольшего возможных значений СВ.
Свойства мат.ожидания:
1. Мат.ожидание постоянной величины равно самой постоянной: М (С) = С.
2. Постоянный множитель можно выносить за знак МО: М (СХ) = СМ (Х).
3. МО суммы 2-х СВ равно сумме МО слагаемых: М (Х + Y) = M (X) + M (Y).
4. МО произведения двух независимых СВ равно произведению их МО:
М (ХY) = M (X) M (Y).
Зная только МО СВ нельзя судить ни о том, какие значения принимает СВ, ни о том, как эти значения рассеяны вокруг мат.ожидания. Т.е. МО полностью не характеризует СВ. Поэтому наряду с мат.ожиданием вводят и другие числовые характеристики. Например, чтобы оценить, как рассеяны величины вокруг МО, используют дисперсию.
Дисперсией СВ называют мат.ожидание квадрата отклонения СВ от ее МО: D (X) = M [ X – M (X)]2 = M (X 2) – [ M (X)]2.
При этом для дискретной СВ: 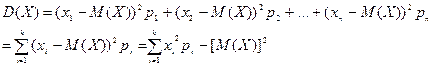 .
.
Для непрерывной СВ: 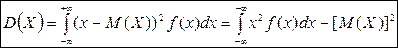 .
.
Замечание. Дисперсия СВ – неслучайная постоянная величина.
Пример 5. Найти дисперсию СВ Х, которая задана законом распределения:
| Х | |||
| р | 0,3 | 0,5 | 0,2 |
Решение. Найдем МО: М (Х) = 1∙0,3 + 2∙0,5 + 5∙0,2 = 2,3.
Затем найдем возможные значения квадрата отклонения:
[ х 1 – M (X)]2 = (1 – 2,3)2 = 1,69; [ х 2 – M (X)]2 = (2 – 2,3)2 = 0,09;
[ х 3 – M (X)]2 = (5 – 2,3)2 = 7,29.
Тогда, D (X) = 1,69∙0,3 + 0,09∙0,5+ 7,29∙0,2 = 2,01.
2 способ. М (Х) = 2,3. Вычислим M (X 2) = 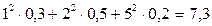 .
.
Искомая дисперсия равна D (X) = 7,3 – (2,3)2 = 7,3 – 5,29 = 2,01.
Свойства дисперсии:
1. Дисперсия постоянной величины равна 0: D (C) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат: D (CX) = C 2 D (X).
3. Дисперсия алгебраической суммы конечного числа независимых СВ равна сумме дисперсий этих величин:
D (X ± Y) = D (X) + D (Y).
Следствие. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины: D (С + Х) = D (X).
Дисперсия имеет размерность, равную квадрату размерности СВ.
Кроме дисперсии для оценки рассеяния СВ вокруг ее среднего значения служат и другие характеристики, например, среднее квадратическое отклонение.
Средним квадратическим отклонением СВ Х называют квадратный корень из ее дисперсии:
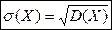 .
.
Размерность сред.квадр.отклонения совпадает с размерностью СВ.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1621; Нарушение авторских прав?; Мы поможем в написании вашей работы!