Назначение Mathcad. Транспортная задача.(Постановка задачи

Транспортная задача.(Постановка задачи. Закрытая модель. Открытая модель.)

Пример

Задача о назначениях

Так называемая задача о назначениях (их можно отнести к задачам о выполнении заказа). Т.е. задача о назначениях может быть отнесена к задачам о распределении заказ.( является частным случаем)

Четверо рабочих могут выполнить четыре вида работ. Стоимость выполнения i-м рабочим j-ой работы приведена в таблице.

	Виды работ
Рабочие

Необходимо составить план выполнения работ так, чтобы все работы были выполнены, каждый рабочий был загружен только на одной работе, а суммарная стоимость выполнения всех работ была минимальной

Отметим, что данная задача является сбалансированной, т.е. число рабочих совпадает с числом выполняемых работ. Если задача не сбалансирована, то перед началом решения ее необходимо сбалансировать, введя недостающее число рабочих (работ) с достаточно большими штрафными стоимостями работ (на порядок выше сомой большой стоимости работ)

Составим математическую модель решения данной задачи. Пусть переменная , если i-м рабочим выполняется j-ая работа, и 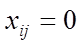, если i-м рабочим не выполняется j-ая работа. Тогда математическая модель будет выглядеть следующим образом:

Целевая функция

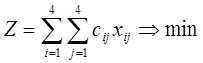
При ограничениях

Решение сбалансированной модели в Excel представлено ниже

12.А.В. Кузнецов, В.А.Сакович, Н.И. Холод. Высшая математика. Математическое программирование., Минск, «Вышэйшая школа», 1994г.286 с., ил

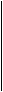При формировании плана выполнения транспортных операций автотранспортного предприятия, осуществляющего грузоперевозки для нужд региона или для группы грузоотправляющих и грузополучащающих предприятий, часто возникают задачи оптимального использования транспортных средств.

Это происходит в связи с тем, что регион может иметь сложную транспортную сеть, позволяющую использовать различные маршруты для выполнения одних и тех же перевозок, многие из которых будут неоптимальными. Однако выяснить это можно только после оценки каждого возможного маршрута по выбранному критерию эффективности, позволяющему однозначно выявлять оптимальный маршрут. Задача значительно усложняется, если необходимо дополнительно учесть грузопотоки между обслуживаемыми предприятиями. Решение таких задач возможно только с использованием специализированного математического аппарата. Опыт показывает, что пренебречь математическими методами оптимизации нельзя при решении даже самых простых задач перевозок. (Линейное программирование)

Линейное программирование позволяет решать не только задачи нахождения оптимальных маршрутов (оптимальных вариантов закрепления грузополучателей за грузоотправителями), но и задачи закрепления автохозяйств за грузовладельцами, выбора типа подвижного состава и распределения его по маршрутам, определения необходимого количества автомобилей, погрузочно-разгрузочных механизмов и др., причем расчеты будут вестись по одному и тому же алгоритму.

Известны следующие методы решения задач линейного программирования: метод северо-западного угла, правило минимального элемента, метод Фогеля, метод потенциалов, симплексный, распределительный, разрешающих множителей и слагаемых и др.

Первые три из перечисленных методов являются достаточно простыми и применяются в основном для решения относительно простых задач или построения опорного плана, который далее необходимо улучшать. Универсальным методом, пригодным для решения задач разных типов, является симплексный метод. Однако он громоздкий и, как правило, требует применения вычислительной техники

Общая методика решения задач линейного программирования — это последовательное улучшение вариантов. Сначала составляется опорный план. Для сокращения объема расчетов он должен быть по возможности близким к оптимальному. Затем по определенному алгоритму отыскиваются новые (лучшие) варианты. Наконец, находят оптимальный вариант.

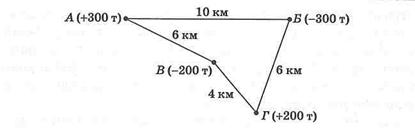
Из грузоотправляющих пунктов А и Г необходимо перевезти груз в грузополучающие пункты В и Б (рис. 5.1). Из пункта А может быть перевезено 300т, из пункта Г — 200т. Расстояния перевозок указаны на рисунке. Необходимо так спланировать перевозки, чтобы общий объем транспортной работы (в тонна-километрах) или среднее расстояние ездки с грузом (в километрах) были минимальными

Можно рассмотреть различные варианты перевозок. На первый взгляд кажется, что наиболее целесообразно весь груз из пункта А доставлять в пункт Б, а из пункта Г — в пункт В. Общий объем транспортной работы при этом составит 300 • 10 + 200 • 4 = 3800 т • км. На самом деле близким к оптимальному варианту перевозок будет следующий: из пункта А в пункт В перевозится 200 т и в пункт Б — 100 т. Из пункта Г перевозится 200 т в пункт Б. Распределение груза осуществлено с учетом наименьших расстояний перевозок.

В этом случае транспортная работа будет равна: 200 • 6 + 100 • 10 + 200 • 6 = 3400 т • км. Среднее расстояние перевозок 1 т груза в первом варианте составляет 7,6 км (3800: 500), во втором — 6,8 км (3400: 500).

Таким образом, при грамотном подходе к решению даже этой простейшей задачи можно добиться снижения объема транспортной работы более чем на 15 %.

Рассмотрим методику определения кратчайших расстояний перевозок из некоторого начального в несколько конечных пунктов, позволяющую находить наилучшие (по пробегу) маршруты перевозок с учетом сложившейся сети дорог. Для каждой пары пунктов, между которыми осуществляется перевозка грузов, возможно движение по разным маршрутам, поэтому все их необходимо сравнивать, чтобы выбрать наилучший (кратчайший). В качестве критерия оптимизации маршрута будем использовать минимальный пробег.

Решать эту задачу можно с помощью теории графов. С формальной точки зрения граф представляет собой упорядоченную пару множеств G = (V, Е), первое из которых дает информацию о количестве и наименовании вершин (узлов) графа, а второе характеризует связывающие их ребра.

При формировании плана автомобильных перевозок для автотранспортного предприятия или группы предприятий на достаточно продолжительный период времени очень важно, чтобы его параметры были близки к оптимальному.

Другими словами, выполнение плана перевозок должно осуществляться с минимумом затрат или (что практически одно и то же) с минимальным общим пробегом либо транспортной работой.

В качестве исходных данных для составления плана используется:

· перечень поставщиков перевозимых продуктов, располагающих определенными запасами;

· перечень потребителей, требующих определенного количества продуктов;

· стоимость перемещения единицы продукта (или расстояние между поставщиками и потребителями).

Реальный план перевозок включает большую номенклатуру поставщиков и потребителей, а соответственно и большое количество связывающих их маршрутов.

Как правило, на АТП эксплуатируется разномарочный подвижной состав, который и будет выполнять эти перевозки, поэтому затраты на перемещение единицы продукта будут разными (затраты на перевозку единицы продукта автомобилем малой или большой грузоподъемности могут различаться в несколько раз). Точно спрогнозировать, каким автомобилем будет осуществлена перевозка, заранее достаточно сложно. Существуют и другие факторы, влияющие на эффективность выполнения плана перевозок: изменение природно-климатических и сезонных условий, дорожная обстановка на маршрутах, большая номенклатура перевозимых грузов, необходимость использования специального подвижного состава, наличие и эффективность работы погрузочно-разгрузочных устройств в пунктах погрузки и выгрузки, объемы минимальных партий перевозок и т.д. Вследствие этого корректно решить поставленную задачу разработки оптимального плана перевозок с использованием аналитических методов расчета не представляется возможным, поскольку таких методов в настоящее время не существует. Поэтому для получения хотя бы приемлемого плана перевозок необходимо упростить поставленную задачу, чтобы можно было применить для её решения известные математические схемы. В качестве принимаемых допущений используют следующие: перемещается однородный продукт, требующий одного и того же подвижного состава; затраты на перемещение единицы продукта постоянны и не зависят ни от каких реально действующих факторов.

Таким образом, задачу формирования оптимального плана перевозок приводят к решению транспортной задачи, которая решается с использованием математической схемы задачи линейного программирования.

Транспортная задача формируется следующим образом.

В m пунктах отправления А₁, …, А_m сосредоточен однородный груз в количествах а₁, …, а_m единиц. Имеющийся груз необходимо доставить потребителям B₁, …, B_n, спрос которых выражается величинами b₁, …, b_n единиц. Известна стоимость перевозки единицы груза из i-го (i=1,m) пункта отправления в j-ый (j=1,n) пункт назначения. Требуется составить план перевозок, который полностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимизируются.

Обозначим через x_{i j} (i=1,m; j=1,n) количество единиц груза, которое необходимо доставить из i-го пункта отправления в j-ый пункт назначения.

Для наглядности условия транспортной задачи можно представить таблицей.

Поставщики	Потребители	Запас груза
В1	В2	…	Вn
А1		с1 1		с1 2	…		с1 n	a1
х1 1		х1 2		…	х1 n
А2		с2 1		с2 2	…		с2 n	a2
х2 1		х2 2		…	х2 n
…	…	…	…	…	…	…	…	…
Аm		сm 1		сm 2	…		сm n	am
хm 1		хm 2		…	хm n
Потребность в грузе	b1	b2		bn

Математическая модель транспортной задачи запишется следующим образом:

ЦФ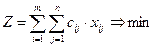

При ограничениях

И граничных условиях

Математическая модель транспортной задачи называется закрытой (сбалансированной), если суммарный объем груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т.е. выполняется равенство

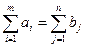
Если для транспортной задачи выполняется одно из условий:

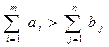
Или

То модель задачи называется открытой (несбалансированной).

Для решения транспортной задачи с открытой моделью необходимо преобразовать ее в закрытую.

Так при выполнении первого условия необходимо ввести фиктивного потребителя В_n+1 спрос которого будет равен

При выполнении второго условия необходимо ввести А_m+1 производителя, объем производства которого будет равен

При этом все тарифы дополнительного потребителя (производителя) чаще всего равны нулю.

Например:

Предположим, что фирма имеет 4 фабрики и 5 центров распределения ее товаров. Фабрики фирмы располагаются в Минске, Борисове, Смоленске и Жодино с производственными возможностями 200, 150, 225 и 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фирмы располагаются в Могилеве, Гомеле, Пружанах, Витебске и Солигорске с потребностями в 100, 200, 100, 250 и 150 единиц продукции ежедневно, соответственно. Хранение на фабрике единицы продукции, не поставленной в центр распределения, обходится в $0,75 в день, а штраф за просроченную поставку единицы продукции, заказанной потребителем в центре распределения, но там не находящейся, равен $2,5 в день. Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в табл. 1.

Таблица 1. Транспортные расходы

	Могилев	Гомель	Пружаны	Витебск	Солигорск
Минск	1,5		1,75	2,25	2,25
Борисов	2,5		1,75		1,5
Смоленск		1,5	1,5	1,75	1,75
Жодино		0,5	1,75	1,75	1,75

Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.

Опорный план – Кузнецов А.В. Математическое программирование (стр 147)

Содержание

Дата добавления: 2014-01-15