История развития

АКУСТО-ОПТИЧЕСКОЕ ВЗАИМОДЕЙТСВИЕ. АКУСТООПТИЧЕСКИЕ ДЕФЛЕКТОРЫ

Лекция 1

Введение

Лекция 22. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ

Лекция 21. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ

Лекция 19. ПАСИВНЫЕ ЭЛЕМЕНТЫ ТРАКТОВ ВОЛС

(часть 2)...................................................................................................................170

Лекция 20.РЕТРАНСЛЯТОРЫ И РЕГЕНЕРАТОРЫ..................................178

(часть 1)...................................................................................................................185

(часть 2)...................................................................................................................197

Лекция 23. ВОЛОКОННО-ОПТИЧЕСКИЕ ГИРОСКОПЫ........................209

Заключение……………………………………………………………………….238

Библиографический список……………………………………………………218

Оптические устройства в радиотехнике изучает устройство и основные характеристики широкого класса оптоэлектронных устройств (модуляторов, фильтров, спектроанализаторов, корреляторов), волоконно-оптические системы передачи, компоненты ВОСП, их основные характеристики и методы их измерения.

Целью курса является ознакомление студентов с широкими возможностями оптоэлектроники, подготовка специалистов в области основ теории и принципов работы оптических устройств обработки информации, а также для проектирования, монтажа, эксплуатации волоконно-оптических линий связи.

Основные задачи курса:

· Получение общих представлений о физических эффектах, лежащих в основе работы оптоэлектронных приборов;

· Получение необходимых знаний по физическим и теоретическим основам функционирования оптических систем передачи и обработки сигналов;

· Изучение физических основ передачи информации по волокну;

· Изучение свойств оптических волокон и кабелей, методов их измерения, внешних факторов, влияющих на их работу;

· Изучение источников и приемников оптического излучения;

· Изучение принципов модуляции и демодуляции оптического излучения;

· Изучение пассивных устройств, ретрансляторов и регенераторов линейных трактов ВОЛС;

Явление дифракции света на ультразвуковой волне было предсказано Бриллюэном в 1922 г., а экспериментально осуществлено в 1932 г. Дебаем, Сирсом, Люка и Бикаром. Бриллюэн предсказал, что частота дифрагированного света должна быть сдвинута за счет эффекта Допплера на величину, равную частоте звуковой волны.

В 1935 - 36 гг. С. В. Раман и Н. С. Нат представили свою теорию дифракции, в первоначальном варианте которой предполагалось, что звуковой столб подобен двумерной фазовой решетке, в которой световые лучи не изменяют своего направления. Такое рассмотрение дало распределение интенсивности света по дифракционным порядкам, описываемое функциями Бесселя, Последующие исследования показали, что эта теория применима лишь для очень узких звуковых столбов, когда волновой параметр Q=λl/Λ²n <<1. В этом выражении λ - длина волны света в вакууме; Λ - длина волны ультразвука; l - длина области взаимодействия света и звука; n - показатель преломления среды. В дальнейших работах Раман и Нат отказались от модели простой фазовой решетки и перешли от волнового уравнения к бесконечной системе связанных дифференциальных уравнений, которые описывают пространственное поведение различных дифракционных порядков при прохождении света через звуковой столб. Эти уравнения были введены для случая малых углов дифракции λ/Λn <<1.

Существенный вклад в исследование дифракции света на ультразвуковых волнах внес С. М. Рытов. Он разработал метод плавных возмущений, позволивший рассчитать интенсивности спектров в случае нормального падения света на ультразвуковой столб.

Интерес к проблеме дифракции света на акустической волне усилился в 50-е и 60-е годы ХХ века, когда проблема была сформулирована в терминах интегральных уравнений, параметрической теории, законов сохранения энергии и импульса фотон - фононного взаимодействия.

В 70-е годы ХХ века появились работы, в которых намечены теоретические методы решения задачи дифракции света на ультразвуке в самой общей постановке.

1.2. Дифракция Рамана – Ната и дифракция Брэгга

Физическая картина дифракции света на упругой волне может быть описана следующим образом. Распространение акустической волны в упругооптической среде сопровождается появлением в этой среде бегущей периодической последовательности изменений показателя преломления. Если период этой последовательности меньше ширины светового пучка, то в среде происходит дифракция света на бегущей со скоростью звука фазовой дифракционной решетке. Характер этой дифракции существенно зависит от длины области взаимодействия света и звука l.

При достаточно малом l (Q=λl/Λ²n <<1) дифракционная решетка может рассматриваться как плоская. В этом случае направления на дифракционные максимумы определяются как в обычной плоской дифракционной решетке.

,

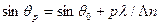где θ_р - направление на р -ый дифракционный максимум, θ ₀ - угол падения света, р – целое число (±1, ±2, ±3,…).

Таким образом, при достаточно малом l дифракционная картина представляет собой набор значительного числа дифракционных максимумов, расположенных симметрично относительно направления падающего света. Такая дифракция называется дифракцией Рамана-Ната, она происходит при любом угле падения света на ультразвуковой столб.

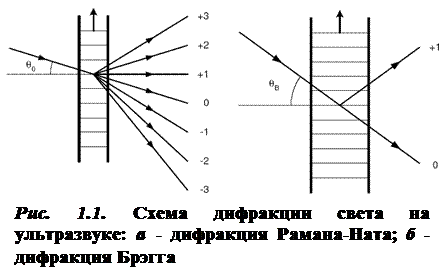
При дифракции Рамана-Ната можно считать, что световой луч проходит через область взаимодействия прямолинейно. Пренебрежение искривлением луча внутри области взаимодействия эквивалентно предположению о чисто фазовой модуляции света при его взаимодействии с упругой волной. Разлагая фазомодулированную волну на выходе из области взаимодействия в угловой спектр, можно получить характерную для дифракции Рамана-Ната картину с большим числом дифракционных максимумов (рис. 1.1, а).

Графики зависимости интенсивности света в нулевом, первом и втором максимумах от параметра ql приведены на рис. 1.2 (где I_i – интенсивность падающего света, I_р - интенсивность продифрагировавшего света в р -ом дифракционном максимуме, 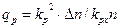, k_p – модуль волнового вектора продифрагировавшей световой волны в р -ом максимуме, k_px -его проекция на ось x, пенпендикулярную направлению распространения ультразвука).

Для дифракции Рамана-Ната характерно наличие значительного числа дифракционных максимумов, симметрично расположенных относительно угла падения света θ ₀. Интенсивности света в симметричных дифракционных максимумах равны.

Амплитуды нескольких первых дифракционных максимумов пропорциональны функциям Бесселя и число таких максимумов тем меньше, чем больше волновой параметр Q. При достаточно больших р амплитуда р -го дифракционного максимума существенно уменьшается. По мере уменьшения l, решение Рамана-Ната становится справедливым для все большего количества дифракционных максимумов.

Существенно иной характер имеет дифракция света на ультразвуке при большой длине l (Q=λl/Λ²n»1). Дифракционная решетка в этом случае является трехмерной и при анализе дифракционной картины необходимо учитывать фазовые соотношения между волнами в направлении длины области взаимодействия. Характер дифракции света на ультразвуковой волне с большим l подобен дифракции рентгеновских лучей на кристаллической структуре. Такая дифракция происходит только при определенном угле падения света на ультразвуковой столб, удовлетворяющем так называемому условию Вульфа-Брэгга.

.

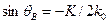Эта дифракция носит название дифракции Брэгга. Для дифракции Брэгга характерно наличие лишь одного дифракционного максимума, который образуется отражением падающего света от фронта бегущей световой волны (рис. 1.1, б).

На рис. 1.3 приведена зависимость I ₁/ I_i от ql для нескольких значений η ₀ l, (η_р = k_px - k_{p +1, x}). С ростом η ₀ l уменьшается максимально достижимое значение I ₁(ql). Изменение η ₀ при заданном угле падения света означает изменение частоты ультразвуковой волны. Параметры большинства акустооптических устройств определяются допустимой полосой изменения частоты акустической волны. Поэтому с помощью соотношения I ₁/ I_i можно оценить предельные возможности многих акустооптических устройств, работающих в режиме Брэгговской дифракции, при заданных допустимых потерях интенсивности света.

При дифракции Брэгга амплитуда и фаза проходящей световой волны существенно зависят от интенсивности ультразвука и величины рассинхронизма акустооптического взаимодействия η ₀. На рис. 1.4 изображены зависимости интенсивности и фазы проходящей световой 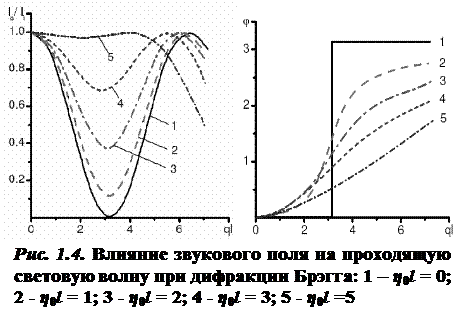волны от интенсивности ультразвука при разных величинах рассинхронизма. При точном выполнении условия Брэгга фаза волны скачком меняется на π при ql = π. При наличии рассинхронизма появляются широкие области плавного и почти линейного изменения фазы от интенсивности ультразвука. Эти зависимости могут быть использованы для фазовой модуляции света акустической волной.

Дата добавления: 2014-01-15