Промежуточный режим дифракции

Режимы дифракции Рамана-Ната и Брэгга представляют собой два предельных случая, соответствующих малым и большим длинам области взаимодействия света и звука. Промежуточный случай умеренных длин области взаимодействия (Q=λl/Λ²n ≈1) является значительно более сложным. Такой режим довольно широко используется в акустооптических устройствах.

Плавный переход между различными режимами дифракции происходит при непрерывном изменении длины l. Таким образом, по мере увеличения l происходит уменьшение числа дифракционных максимумов и сужение допустимых пределов углов падения света. Строгие границы режимов дифракции не могут быть установлены из-за того, что число дифракционных максимумов существенно зависит от мощности ультразвуковой волны Р_а, вызывающей дифракцию света. С увеличением Р_а число дифракционных максимумов растет.

На рис. 1.5 приведена зависимость относительной интенсивности света в первом максимуме от величины ql при различных Q и угле падения света, совпадающем с углом Брэгга.

При ql< 1,5 эффективность дифракции в первый максимум не зависит от Q, а при 1,5< ql< 4,5 монотонно увеличивается с ростом Q. При Q >1,5 может считаться достигнутым брэгговский режим дифракции. Интересно отметить, что при Q =0,64 эффективность дифракции составляет ~ 60% при изменении ql в широких пределах от 2,5 до 6,5.

На рис. 1.6 приведены зависимости относительной интенсивности в первом дифракционном максимуме от угла падения света для различных Q и ql = 4. С помощью этого графика можно оценить угловую избирательность дифракции в промежуточной области.

Угловая зависимость тесно связана с зависимостью интенсивности света от частоты акустической волны, поскольку 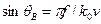, где f - частота акустической волны, а v - ее скорость в среде. Если учесть еще и квадратичную зависимость Q от f, то получится частотная зависимость интенсивности света в первом дифракционном максимуме, изображенная на кривой 7 рис. 1.6.

На рис 1.7 изображена зависимость интенсивности света во втором дифракционном максимуме от ql в области промежуточных Q. При 0,65 < Q < 0,8 эффективность дифракции во второй максимум достигает более 65% при 4 < ql < 5. Эти кривые рассчитаны для случая угла падения света, равного удвоенному углу Брэгга.

Угловая зависимость интенсивности второго дифракционного максимума приведена на рис. 1.8 для случая ql = 5. Сравнение рис. 1.8 и рис. 1.6, а также рис.1.7 и рис. 1.5 показывает, что использование второго дифракционного максимума может быть достаточно эффективно при значениях Q несколько меньше единицы, если не важна линейность зависимости I_d от ql.

Дата добавления: 2014-01-15