Лінійні операції над векторами

1. Додавання векторів

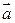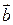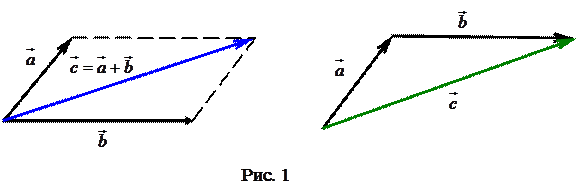
Сумою двох векторів і називають такий третій вектор 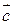, який виходить з їх спільного початку, і є діагоналлю паралелограму, сторонами якого служать додатки векторів (рис. 1).

Правило додавання векторів: щоб додати два вектора 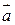і 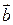треба, пересуваючи вектор 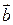паралельно самому собі сполучити його початок з кінцем вектора 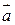. Тоді сума 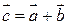є вектор, що йде з початку 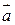в кінець .

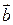Із правила додавання двох векторів можна отримати правило додавання любої кількості векторів.

Сума любої кінцевої кількості векторів зображується відрізком, замикаючим ломану, ланками якої служать доданки вектори. Напрям результуючого вектора береться від початку першого доданку вектора до кінця останнього.

2. Віднімання векторів

Різницею двох векторів 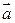і 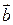називається такий третій вектор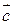, для якого сума 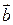і 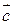дорівнює 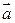(рис. 2).

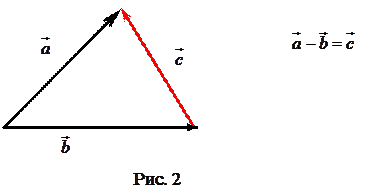Таким чином, щоб з одного вектора відняти другий, треба віднести їх до спільного початку і провести вектор із кінцевої точки вектора-від’ємника в кінцеву точку вектора-зменшуваного.

3. Множення вектора на число

Додаючи декілька рівних векторів, тобто повторюючи вектор доданком декілька разів ми приходимо до множення його на додатне ціле число. Згідно означення маємо: .

При множенні вектора 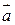на число 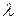довжина вектора множиться на 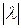, а напрямок зберігається старий, якщо 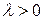і змінюється на протилежний, якщо .

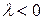Приведемо закони множення вектора на число:

1) ; ; ; ;

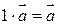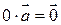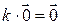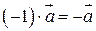2) ;

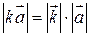3) , ;

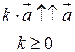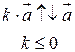4) асоціативний закон ;

5) дистрибутивний закон відносно скалярних множників ;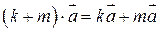

6) дистрибутивний закон відносно векторів .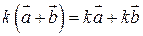

Дата добавления: 2014-01-11