Скалярні і векторні величини. Лінійні операції над векторами: складання і віднімання векторів, множення вектора на число, проекція вектора на вісь

Лекція № 1

Тема: Вступ. Вектори. Лінійні операції над векторами. Проекція вектора на вісь. Розклад вектора по ортонормованому базису. Напрямні косинуси. Довжина вектора

Питання лекції:

1. Скалярні і векторні величини. Лінійні операції над векторами: складання і віднімання векторів, множення вектора на число, проекція вектора на вісь.

2. Лінійна залежність і незалежність векторів, базис. Розкладання вектора по ортонормованому базису. Довжина вектора. Напрямні косинуси.

Величини, з якими ми зустрічаємося в механіці, фізиці і в інших прикладних дисциплінах бувають подвійного значення: скалярні і векторні.

Приклади скалярних величин: площа, об’єм, довжина відрізка, маса, час і т.п.

Приклади векторних величин: сила, момент, швидкість, прискорення, і т.п.

Величина, яка характеризується числовим значенням і напрямком, носять назву – вектора.

Числове значення вектора називається його модулем. Позначається , .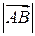

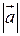Графічно вектор позначають відрізком зі стрілкою на кінці. Довжина відрізка у вибраному масштабі відповідає модулю вектора. Стрілка вказує напрямок.

Вектор, модуль якого дорівнює одиниці, має назву – одиничного (ще його називають ортом). В подальшому будемо зустрічатися з таким поняттям як ортонормований базис.

Вектор, модуль якого дорівнює нулю, носить назву нульового.

Два вектори вважаються рівними, якщо вони мають однакову довжину, паралельні і направлені в один і той же бік.

Вектори, рівні по модулю, паралельні, але мають напрямки в протилежні боки називаються – взаємо протилежними.

На відміну від векторів, величини які не мають напрямку називаються – скалярами.

Дата добавления: 2014-01-11