Анализ структуры уравнений движения трехстепенного гироскопа в инерциальной системе координат и их линеаризация

Лекция 6

Таким образом, поведение трехстепенного гироскопа в инерциальной системе координат в режиме номинального вращения гиромотора как электрической машины, полученное тремя методами: Лагранжа, Эйлера и Даламбера, описывается системой нелинейных дифференциальных уравнений

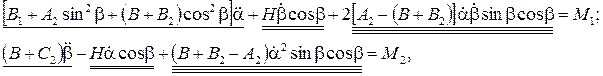(6.1)

где 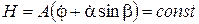- кинетический момент ротора гиромотора гироскопа; члены, подчеркнутые одной чертой, являются составляющими обычного инерционного момента М _ин,; члены, подчеркнутые двумя чертами, являются гироскопическими моментами М _г1, обусловленными кинетическим моментом ротора гиромотора гироскопа; члены, подчеркнутые тремя чертами, являются гироскопическими моментами М _г2, обусловленными кинетическими моментами рамок гироскопа (при этом указанные моменты взяты с обратными знаками).

Для исследования поведения гироскопа необходимо задать внешние моменты 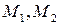и начальные условия 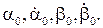Однако даже при 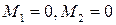система (6.1) не интегрируется, поэтому для ее решения применяются различные приближенные методы [ ].

При анализе технических приложений гироскопа необходимо определить, когда можно использовать полные дифференциальные уравнения движения гироскопа, а когда допустимо использовать его технический аналог (приближенные уравнения – линеаризованные).

Если нас интересует динамический дрейф [], то нужно использовать полные уравнения движение гироскопа. Если пренебречь в уравнениях (6.1) составляющими, обусловленными кинетическими моментами рамок гироскопа (члены, подчеркнутые тремя чертами – такое приближение можно сделать вследствие того, что 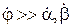), то получим технические уравнения движения гироскопа

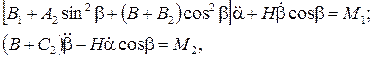(6.2)

которые также не интегрируются в элементарных функциях. Проведем линеаризацию этих уравнений относительно начального положения

, , ,

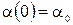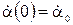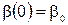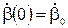
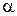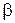В технических приложениях углы и меняются относительно некоторых начальных значений очень незначительно. Поэтому углы отклонения представить в виде

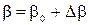, , (6.3)

где 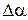, 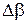- малые отклонения от начального положения.

Тогда выражения для производных примут вид

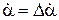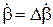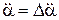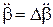, , , (6.4)

Проведем линеаризацию тригонометрических функций

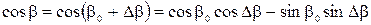
Отсюда в силу малости отклонения 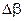, получим

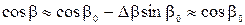(6.5) По аналогии

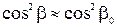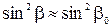, (6.6) Подставив формулы (6.4)-(6.6) в (6.2), получим линеаризованные технические уравнения движения гироскопа

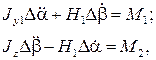(6.7)

где 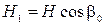- активная составляющая кинетического момента гироскопа; 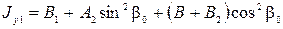- момент инерции относительно оси подвеса наружной рамки, обусловленный всеми элементами конструкции; 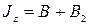- суммарный момент инерции относительно оси подвеса внутренней рамки.

Если в уравнениях (6.7) пренебречь инерционными моментами, то получим прецессионные уравнения движения гироскопа

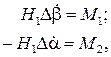(6.8)

которые используются в различных технических приложениях, когда нутационными колебаниями можно пренебречь (см. ниже).

Дата добавления: 2014-01-15