КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Анализ различных видов движения трехстепенного гироскопа
|
|
|
|
Движение гироскопа по инерции (нутация гироскопа).
Постановка задачи: имеем систему (6.7), начальные условия для которой могут быть представлены в виде
 ,
, 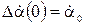 ,
,  ,
, 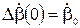 .
.
Так как рассматриваем чисто движение по инерции, то 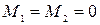 .
.
Найти 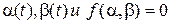 .
.
Таким образом, имеем следующую систему дифференциальных уравнений нутационного движения гироскопа
 (6.9)
(6.9)
Рассмотрим возможные методы решения данной системы:
1.Метод решения систем дифференциальных уравнений. Заключается в решении системы, содержащей 4 переменных.
2.Решение операторным методом. То есть  ,
,  .
.
Задание: записать систему уравнений в операторной форме.
3.Сведение системы уравнений к одному уравнению.
Решаем данную систему третьим способом.
Из второго уравнения системы (6.9) имеем:
 (6.10)
(6.10)
 (6.11)
(6.11)
 (6.12)
(6.12)
Подставив (6.11) в первое уравнение системы (6.9), получим:
 , (6.13)
, (6.13)
где 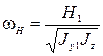 - круговая частота нутационных колебаний.
- круговая частота нутационных колебаний.
Составим характеристическое уравнение для данного дифференциального уравнения
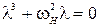 ,
,
корни которого равны 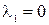 ,
,  .
.
По виду корней характеристического уравнения составляем решение
 . (6.14)
. (6.14)
Отсюда
 . (6.15)
. (6.15)
Подставляем (6.15) в (6.12) и находим выражение для 
 . (6.16)
. (6.16)
Продифференцируем это выражение
 . (6.17)
. (6.17)
Исходя из начальных условий, найдем константы интегрирования 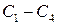 . Для этого рассматривая уравнения (6.14) – (6.17) в момент времени t = 0, составим систему алгебраических уравнений относительно неизвестных констант
. Для этого рассматривая уравнения (6.14) – (6.17) в момент времени t = 0, составим систему алгебраических уравнений относительно неизвестных констант 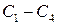
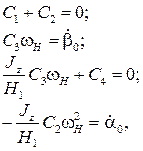
решая которую, получим
 ,
, 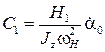 ,
,  ,
, 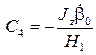 .
.
С учетом  значения констант принимают вид
значения констант принимают вид
 ,
, 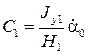 ,
,  ,
, 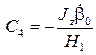 .
.
Подставив найденные константы интегрирования в уравнения (6.14) и (6.16), найдем окончательное решение исходной системы дифференциальных уравнений

Перепишем полученное решение иначе
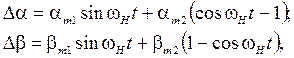 (6.18)
(6.18)
где 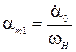 ,
, 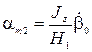 ,
, 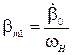 ,
, 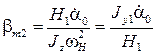 .
.
Интерпретация нутационного движения гироскопа на картинной плоскости.
1. На векторе  в начальном положении откладываем единичный вектор
в начальном положении откладываем единичный вектор 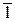 (полученную точку называют апексом).
(полученную точку называют апексом).
2. Вводим прямоугольную систему координат  с началом в
с началом в 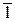 (точке с координатами
(точке с координатами  ).
).
3. Исключаем в (6.18) время: сначала преобразуем, а затем возводим в квадрат и складываем

где

 ;
;
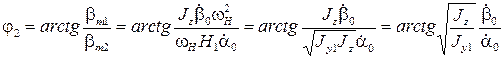 .
.
Т.е. 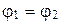 и, следовательно,
и, следовательно,
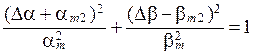 . (6.19)
. (6.19)
Полученное выражение есть уравнение эллипса, центр которого смещен по координатам  соответственно на
соответственно на 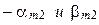 , а полуоси эллипса соответ-ственно равны
, а полуоси эллипса соответ-ственно равны  .
.
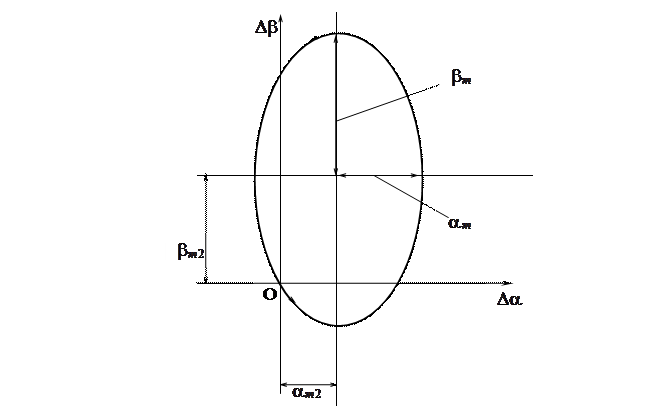
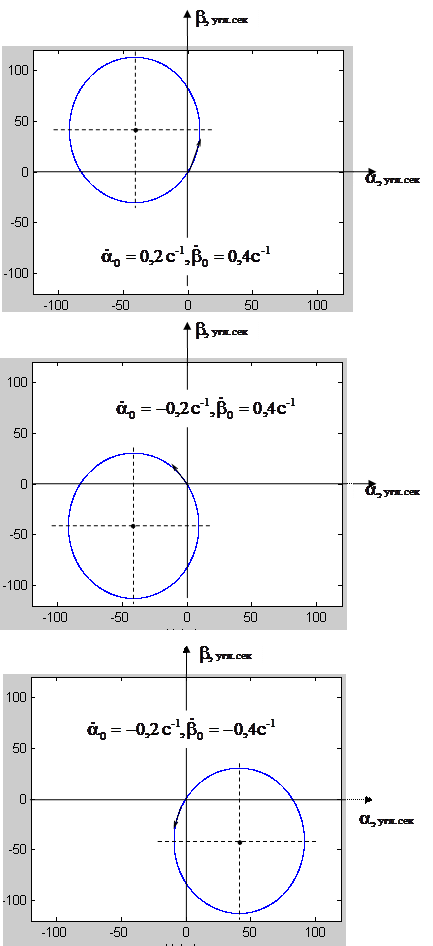
Траектория оси ротора, соответствующая уравнению (19), приведена на рис.1
|
Замечания.
1. О направлении движения по эллипсу.
Движение происходит из начала координат против часовой стрелки.
2. В зависимости от знаков начальных условий  координаты центра эллипса будут находиться в одном из четырех квадрантов.
координаты центра эллипса будут находиться в одном из четырех квадрантов.
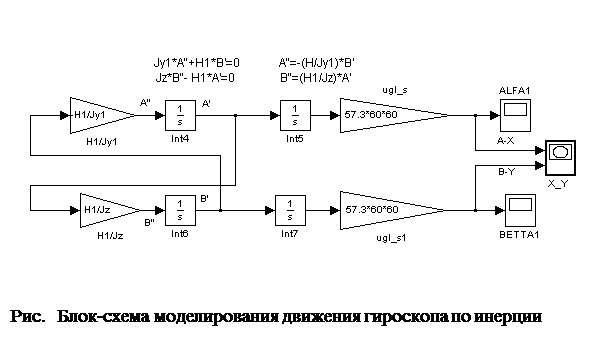
В приложении к лекции №6 приведена схема моделирования в Simulinke программы Matlab и траектории апекса гироскопа при различных начальных условиях по скоростям  .
.
Приложение к лекции №6.
Исходные данные - параметры гироскопа.
J y1=4 - момент инерции относительно оси наружной рамки (Гсмc2);
J z=2 - момент инерции относительно оси внутренней рамки (Гсмc2);
H =4000 - кинетический момент гироскопа (Гсмс);
H 1=4000 - кинетический момент - активная
составляющая Н1 = Н cos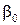 (Гсмс);
(Гсмс);
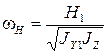 -круговая частота нутационных колебаний;
-круговая частота нутационных колебаний;
NUA=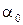 ; NUB=
; NUB=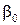 - начальные условия по угловым скоростям задаются
- начальные условия по угловым скоростям задаются
на int4 и int6.
| |||||||
 | |||||||
 | |||||||
 |
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1012; Нарушение авторских прав?; Мы поможем в написании вашей работы!
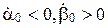 , причем
, причем 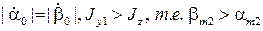
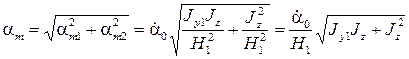
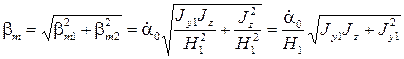 и
и 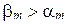 .
.