Шкала порядка, шкала интервалов

В этом случае обычно данные пред­ставляют в сгруппированном виде, так как иначе об­разуется очень много классов. Например, мы иссле­дуем возрастной состав той же группы из тридцати человек. Если она не однородна в этом отношении, данные окажутся «размазанными». Тогда мы их группируем, выбирая определенный шаг (обычно десять лет), и вносим в таблицу обобщен­ные данные. Шаг выбирается с учетом характера данных и задач анализа. Отметим, что группировка данных приводит к потере части информации. Но зато мы добиваемся ее лучшей обозримости. Таб­лица распределения, которая в результате получится, может выгля­деть так:

Таблица 2. Данные о возрастном составе группы авторов

Возрастная группа	Частоты	%	Накопленные частоты	Накопленные %
20-29		40,0		40,0
30-39		26,7		66,7
40-49		16,7		83,4
50-59		9.9		93,3
60-69		6,7		100,0
Всего		100,1		100,0

В первом столбце представлены возрастные интер­валы. Обратим внимание, что они не пересекаются, то есть мы берем интервалы 20 — 29, 30 — 39, а не 20 — 30, 30 — 40. Иначе неясно будет, куда относить ин­дивидов, попадающих на стык возрастных групп. Во втором и третьем столбцах представлены соответ­ственно частоты и проценты. Глядя на них, мы видим, что возрастной состав группы неоднородный: в ней преобладают молодые люди, а люди старших возрас­тов встречаются реже.

В четвертом и пятом столбцах частоты и проценты представлены в несколько иной форме, которая при­менима для упорядоченных категорий (шкал порядка или отношений). Частоты и проценты суммируются по всем предыдущим категориям. При такой форме представления данных хорошо видно, сколько человек или какая доля выборки находятся ниже (или выше) опре­деленного уровня. В нашем примере 25 человек из 30, или 83,4 %, моложе пятидесяти лет.

2) Данные о распределении переменной пред­ставляем в форме гра­фиков. Рассмотрим четыре типа графиков, которые чаще всего используются в случае одномерного распределения.

Для шкал наименований обычно применяют столбиковые диаграммы. Число столбиков соответствует числу категорий. Высота каждого стол­бика отражает частоту встречаемости данной катего­рии. Все столбики рисуются одинаковой ширины и не соприкасаются друг с другом. Порядок их расположе­ния на горизонтальной оси может быть любым. Для представления долей и процентов удобны круго­вые диаграммы. Весь круг соответствует единице или ста процентам, а величина каждого сектора отражает представительство соответствующей категории.

Рис. 1. Столбиковая диа- Рис. 2. Круговая диаграмма

грамма (Данные из Табл.1) (Данные из Табл. 1)

Для наглядного представления измеренных данных шкал равных интервалов используются так называ­емые гистограммы и полигоны. Гистограмма похожа на столбиковую диаграмму, только на горизонтальной оси в этом случае указываются границы интервалов. Столбики примыкают друг к другу. Высота столбика соответствует наблюдаемой частоте. Гистограмму лег­ко преобразовать в полигон. Для этого середины вер­шин каждого столбца соединяются между собой прямыми отрезками. Получается ломаная линия, повторя­ющая контур, образуемый столбиками. Гистограмма удобна для изображения особенностей одного распре­деления. Преимущество полигона заключается в том, что на одном графике можно представить несколько полигонов и затем сравнивать между собой разные выборки.

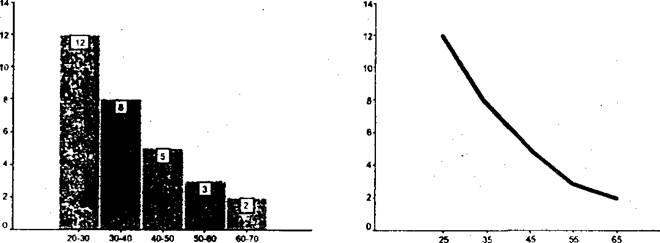
Возрастные группы Возрастные группы

Рис. 3. ГистограммаРис. 4. Полигон

3) Оценка параметров распределения.

Построение таблиц и графиков — это первый шаг статистического анализа. Следующим шагом является оценка параметров распределения. Вычисляются пока­затели, которые позволяют дать еще более сжатое опи­сание наблюдаемых значений.

Эти показатели распада­ются на две основные группы: 1) меры центральной тен­денции;

2) меры рассеяния.

1) Меры центральной тенденции. Ониуказывают на расположение среднего, или типичного, значения признака, вокруг которого сгруппированы остальные наблюдения. Понятие среднего, цент­рального, значения в статистике, как и в повседневной жизни, под­разумевает нечто «ожидаемое», «обычное», «типичное». Наиболее часто используют так называемое среднее (арифметическое). Вычисляют его, как известно, путем суммирования значений всех на­блюдений и деления полученной суммы на общее число наблюдений. Для числовой шкалы:

то есть

где X₁…X_i – наблюдаемые значения, n – число наблюдений.

В случае сгруппированных данных (шкала интервалов) посту­пают следующим образом: находят середину каждого интервала, это значение умножают на частоту, получен­ные величины складывают и делят на общее число наблюдений. Рассматриваемый показатель характеризует область распределения, в которой концентрируются наиболее типичные представители изучаемой выборки. Но это справедливо лишь для тех случаев, когда распре­деление близко к нормальному. При таком распределе­нии основная масса значений концентрируется в его средней части, а любые отклонения встречаются тем реже, чем дальше они отстоят от центра. Например, распределение такого признака, как рост человека, в целом близко к нормальному: больше всего людей среднего роста, а очень высокие и очень маленькие по­падаются довольно редко. Средняя величина удобна для сравнения двух выборок или двух популяций. Так, мы говорим, что мужчины в среднем выше женщин, и это утверждение вполне справедливо несмотря на то, что встречаются высокие женщины, рост которых значи­тельно превышает среднестатистический. Или, напри­мер, известно, что средний рост мужчины-пигмея мень­ше роста средней европейской женщины.

Две другие меры центральной тенденции — это мо­да (Мо) и медиана (Мd). В качестве моды берется значение, кото­рое чаще всего встречается в распределении. Моду специально вычислять не надо. Достаточно сгруппиро­вать данные и выбрать тот класс, в который попадает больше всего наблюдений. В разобранном выше при­мере (Табл. 1) лучше всего представлена категория се­мейных людей. Это и есть мода для данной выборки. Встречаются распределения, име­ющие не одну, а две моды. Распределение такого типа называется бимодальным. На графике в этом случае мы увидим две вершины. Чаще всего это указывает на то, что выборка является неоднородной: в ней присут­ствуют два типа объектов. Констатация такого факта обычно наводит нас на мысль разбить всю выборку на две подгруппы и рассмотреть их отдельно.

Медиана (Md) — это значение, которое делит упорядоченное множество данных пополам, так что одна половина наблюдений оказывается меньше медианы, а другая — больше. Иными словами, медиана — это 50-й процентиль распределения. Как мы уже видели, при работе с большим массивом данных удоб­нее всего искать медиану, построив на основании частотного рас­пределения распределение накопленных частот (или построив рас­пределение накопленных процентов на основании распределения процентов). Если число значений в группе наблюдений чет­ное, то медианой будет среднее двух центральных значений.

Когда распределение имеет нор­мальный вид (то есть оно симметрично), его среднее арифметическое значение и медиана совпадают. Ког­да же распределение асимметрично (скошено), медиа­на лучше схватывает его центральную тенденцию. Выбор подходящей меры центральной тенденции определяется как характером распределения, так и характером используемых данных.

Качественные дан­ные (шкала наименований) допускают использование только моды. Для ранжированных данных (шкала порядка) допустимо использование и моды, и медианы. Количественные данные (шкала равных интервалов) можно описывать любым из трех показателей, хотя на практике чаще всего в этом случае вычисляют среднее арифметическое значение. Именно этот показатель вместе с показателем рассеяния участвует в расчете целого ряда других статистических показателей.

Дата добавления: 2014-01-15