Формули Бейеса

Наслідком теорем множення ймовірностей та формули повної ймовірності є так звані формули Бейеса. Нехай маємо повну групу попарно несуміснх подій 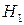, ,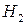..., . 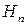Ймовірності цих гіпотез до досліду відомі і дорівнюють відповідно 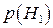, ,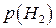..., . 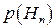Після проведення досліду спостерігалася поява деякої події 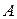. Треба переоцінити гіпотези 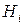після того, як відбулася подія 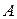, тобто треба визначити умовні ймовірності кожної гіпотези, тобто обчислити 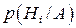. За теоремою множення ймовірностей, маємо:

.

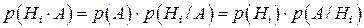
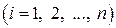звідки

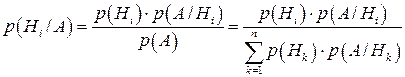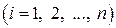, (2)

Формули (2) носять назву формул Бейеса, або теорем гіпотез.

Приклад 6. Для участі в студентських відбіркових спортивних змаганнях виділено з І групи курсу 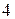студента, з П групи курсу – 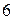і з Ш – 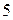студентів. Ймовірність того, що студент І, П, і Ш групи потрапить до збірної інституту відповідно дорівнює 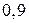; 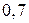і 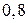. Навмання відібраний студент по результатам змагань потрапив до збірної. До якої групи найімовірніше усього належав цей студент?

Розв’язання. Подія 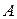– студент потрапив до збірної.

Нехай 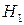– подія, що полягає в тім, що студент з І групи, 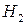– подія, що полягає в тім, що студент з П групи; 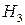– подія, що полягає в тім, що студент з Ш групи.

Ймовірність гіпотез:

; ; .

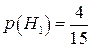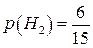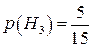Умовні ймовірності:

; ; .

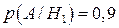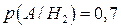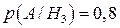Тоді застосовуючи формули Бейеса, отримаємо

;

;

.

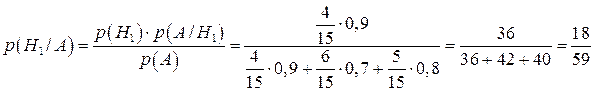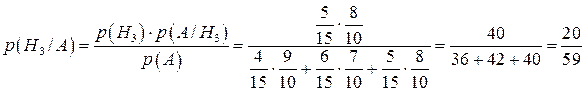Висновок: Найімовірніше це був студент П групи.

Приклад 7. приладів складає спеціаліст високої кваліфікації і – середньої. Надійність роботи приладу складеного спеціалістом високої кваліфікації 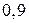, а середньої – 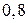. Взятий навмання прилад виявився надійним. Обчислити ймовірність того, що його склав спеціаліст високої кваліфікації.

Розв’язання. Позначимо через 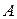подію, яка полягає в тому, що прилад, взятий навмання виявився надійним. Через 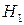– позначимо гіпотезу, що прилад склав спеціаліст високої кваліфікації, а через 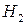– середньої кваліфікації. Тоді ; ; ; .

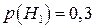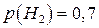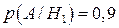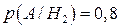Використовуючи формули Бейеса визначимо ймовірність того, що прилад склав спеціаліст високої кваліфікації:

.

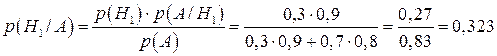А ймовірність того, що цей прилад склад спеціаліст середньої кваліфікації можна визначити або за формулами Бейеса, або як ймовірність протилежної події.

.

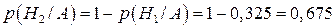Приклад 8. На радіозаводі виготовляються резистори на трьох автоматах. Перший автомат виробляє 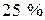, другий – 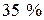, третій – 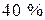усіх резисторів. Відсоток (процент) браку відповідно першого, другого і третього автоматів складає 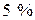, , 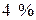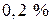. Обчислити ймовірність того, що навмання взятий придатний резистор виготовлений відповідно першим, другим і третім автоматом.

Розв’язання. Позначимо через 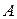подію, яка полягає в тому, що взятий навмання резистор придатний. Через 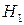позначимо гіпотезу, яка полягає в тому, що резистор виготовлений першим автоматом, через 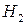– другим автоматом і 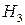– третім автоматом. Тоді 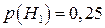; ; 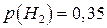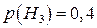. Умовні ймовірності ; ; .

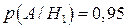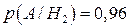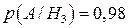За формулами Бейеса:

.

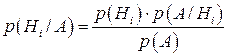
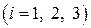Обчислимо спочатку повну ймовірність

.

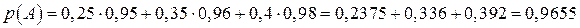Тоді

;

;

.

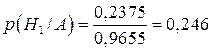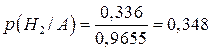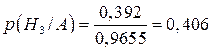Приклад 9. В будівельному загоні першокурсників і студентів другого курсу. Серед першокурсників дівчат, а серед студентів другого курсу 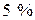дівчат. Всі дівчата по черзі чергують на кухні. Обчислити ймовірність того, що у випадково вибраний день на кухні чергує першокурсниця.

Розв’язання. Позначимо через 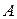подію, яка полягає в тому, що на кухні чергує дівчина. Нехай 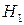– гіпотеза, яка полягає в тому, що вона першокурсниця, а 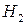– гіпотеза, яка полягає в тому, що вона студентка другого курсу. Тоді 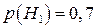; ; ; 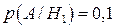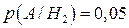. Тоді за формулами Бейеса

.

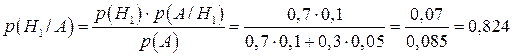Приклад 10. В групі з студентів, які прийшли на іспит три підготовлені відмінно, чотири – добре, два – задовільно і один – незадовільно. В екзаменаційних білетах 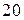питань. Відмінно підготовлений студент може відповісти на всі 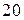питань; студент, який підготовлений на добре може відповісти на 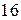питань. Студент, який підготовлений посередньо, може відповісти на питань. А студент, який вчиться погано може відповісти тільки на 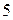питань. Викликаний навмання студент відповів на три довільно задані питання. Обчислити ймовірність того, що цей студент підготовлений 1) відмінно; 2) погано.

Розв’язання Позначимо через 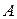подію, яка полягає у тому, що навмання викликаний студент відповів на три питання. Позначимо через 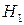– гіпотезу, що полягає в тому, що студент підготовлений відмінно, через 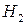– добре, через 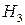– посередньо, через 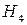– погано. Тоді 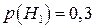; ; 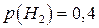; 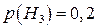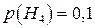. Умовні ймовірності .

За теоремою множення ймовірностей:

;

;

.

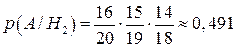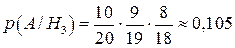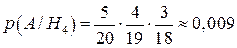Отже, за формулами Бейеса:

;

; ; .

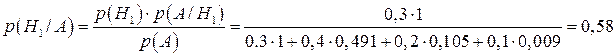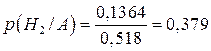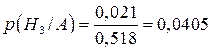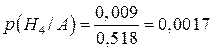Приклад 11. Якийсь чоловік заблукав у лісі і вийшов на галявину, з якої вело 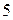доріг. Відомо, що ймовірність виходу з лісу за годину для різних доріг різні і дорівнюють відповідно 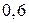; ; 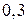; ; 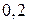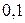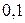. Обчислити ймовірність того, що чоловік пішов по першій дорозі, якщо відомо, що він вийшов з лісу через годину.

Розв’язання. Позначимо через 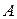подію, яка полягає в тому, що чоловік вийшов з лісу через годину. Через 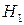позначимо гіпотезу, що він пішов по І дорозі, через 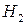, , 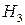, 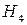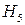– по П, Ш, ІV, V відповідно. Тоді .

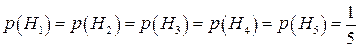Умовні ймовірності ; ; ; .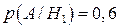

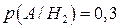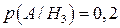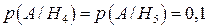Тоді за формулами Бейеса

.

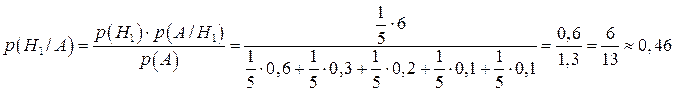Дата добавления: 2014-01-11