Формула повної ймовірності

Тема: Формула повної ймовірності. Ймовірність гіпотез. Формули Бейеса

Лекція № 4

Питання лекції:

1. Формула повної ймовірності.

2. Формули Бейеса.

При обчисленні ймовірностей складних подій часто з’являється потреба сумісно застосовувати теореми додавання та множення ймовірностей. Нехай треба обчислити ймовірність деякої події 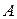, яка може відбутися з однією з подій 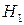, ,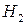..., , 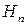які утворюють повну групу попарно несумисних подій. Так як заздалегідь невідомо з якою з подій 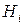відбувається подія 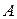, то події 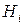називаються гіпотезами. Тоді ймовірність події 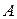визначається (обчислюється) за формулою повної ймовірності.

Ймовірність події 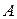дорівнює сумі добутків ймовірностей кожної гіпотези на умовну ймовірність події 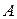при цій гіпотезі, тобто

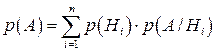(1)

Приклад 1. В радіомайстерні є п’ять однакових коробок з діодами. Дві коробки по 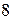діодів, виготовлених заводом і три коробки по діодів у кожній, виготовлених заводом . В коробці, де діоди виготовлені заводом , шість придатних і два бракованих діоди. В коробці, де діоди виготовлені заводом , сім придатних і три бракованих. Навмання вибирають коробку і з неї навмання беруть діод. Обчислити ймовірність того, що взятий діод придатний.

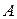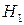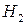Розв’язання. Позначимо через подію, яка полягає в тому, що взятий навмання діод придатний, через – подію (гіпотезу), що діод виготовлений заводом , через – подію (гіпотезу), що діод виготовлений заводом . Так як придатний діод може бути або з коробки, де діоди виготовлені заводом №1 або №2. Тоді , або за формулою повної ймовірності

,

де ; ; ; .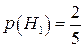

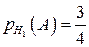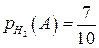Тоді

.

Приклад 2. На зборку механізму надходять однакові деталі з чотирьох цехів. З першого цеху надходять тридцять деталей, з другого – двадцять, з третього – п’ятдесят, з четвертого – двадцять п’ять деталей. Ймовірність браку в кожному з цехів відповідно дорівнює: ; ; ; .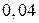

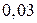Обчислити ймовірність того, що взята навмання деталь буде бракованою.

Розв’язання. Позначимо через 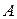подію, яка полягає в тому, що взята навмання деталь бракована. Позначимо через 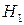– гіпотезу, яка полягає в тому, що деталь виготовлена цехом , через 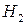– цехом ; через 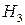– цехом 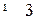і через 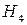– цехом .

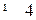Усіх деталей надійшло 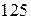штук, тоді ймовірності гіпотез:

; ; ; .

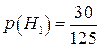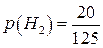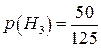Умовні ймовірності дорівнюють:

; ; ;

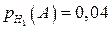Тоді застосувавши формулу повної ймовірності, отримаємо

.

.

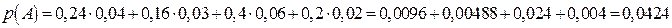Приклад 3. В групі 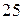студентів, п’ять з них навчаються тільки на відмінно, десять студентів навчаються на добре і десять навчаються слабо. Відмінники на майбутньому іспиті можуть отримати тільки відмінні оцінки. Студенти, які навчаються на добре з однаковою ймовірністю можуть отримати оцінки добре або відмінно. Студенти, які навчаються слабо, можуть з однаковою ймовірністю отримати оцінки добре, задовільно або незадовільно. Для складання іспиту викликається навмання один студент. Обчислити ймовірність, що студент отримає оцінку відмінно або добре.

Розв’язання. Позначимо через 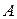подію, яка полягає в тому, що студент отримає оцінку добре або відмінно. Позначимо через 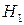гіпотезу, що викликаний студент відмінник, через 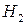– гіпотезу, що викликаний студент навчається на добре і через 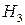– гіпотезу, що викликаний студент навчається на слабо, тоді

; ; .

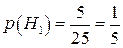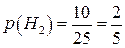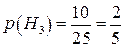Умовні ймовірності того, що студент отримає відмінно, якщо він відмінник . Аналогічно ; .

Тоді за формулою повної ймовірності

.

Приклад 4. Лиття у болванках для подальшої обробки надходить з двох заготівельних цехів, з першого цеху – , а з другого – . Причому болванки, які надходять з першого цеху мають , а з другого 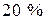браку. Обчислити ймовірність того, що взята навмання болванка не має вади (дефекту).

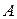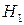Розв’язання. Позначимо через подію, яка полягає в тому, що навмання взята болванка має ваду (дефект). Тоді – не має вади. Нехай – гіпотеза, що болванка з першого цеху, а 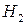– з другого. Тоді

;

.

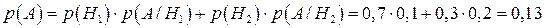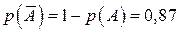Приклад 5. На першому заводі на кожні лампочок виробляється в середньому 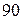стандартних, на другому – , на третьому – 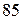, а продукція їх складає відповідно 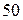, і 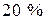всіх електролампочок, що постачаються в магазини даного району. Знайти ймовірність набуття стандартної електролампочки.

Розв’язання. Нехай 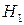подія, яка полягає в тому, що отримана лампочка виготовлена на І заводі; 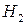– подія, яка полягає в тому, що отримана лампочка виготовлена на П заводі; 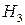– подія, яка полягає в тому, що отримана лампочка виготовлена на Ш заводі.

Ймовірність гіпотез: ; ; .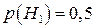

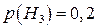Умовні ймовірності події 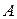відносно кожної з ймовірностей дорівнюють:

; ; .

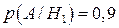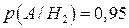Застосувавши формулу повної ймовірності отримаємо

Дата добавления: 2014-01-11