Найімовірніше число появи подій

Інколи на практиці треба знати, яке число появи події 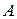в серії 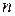повторних незалежних дослідів є найімовірнішим, тобто при якому 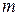ймовірність 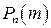найбільша. Це число 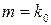називається найімовірнішим числом появи події 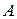. Можна довести, користуючись формулою (2), що найімовірніше число появи події 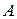визначається з подвійної нерівності

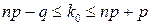(3)

при цьому:

а) якщо число 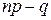– дріб, то існує одне найімовірніше число ;

б) якщо число 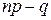– ціле, то існує два найімовірніших числа, а саме: і ;

в)якщо число 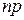– ціле, то найімовірніше число .

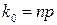Приклад 1. Схожість насіння деякої рослини складає 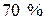. Обчислити ймовірність того, що з десяти посіяних насінин зійде: 1) насінин; 2) не менше восьми насінин.

Розв’язання. З умови задачі , , , .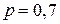

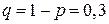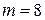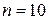1) за формулою Бернуллі маємо:

.

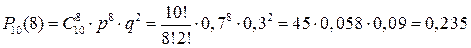2) Якщо через 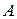позначити подію, що зійде не менше насінин, то за теоремою додавання ймовірностей

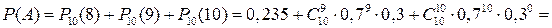
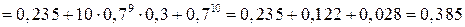
Приклад 2. Серед волокнин бавовни в середньому буває коротких і 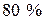– довгих. Обчислити ймовірність того, що в жмуті з шести волокнин: 1) два коротких; 2) не більше двох коротких волокнин.

Розв’язання. За умовою задачі , , , .

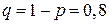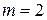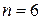1) За формулою Бернуллі:

.

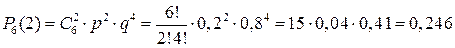2) За теоремою додавання ймовірностей

.

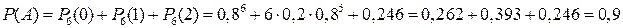Приклад 3. В майстерні є шість електродвигунів. Для кожного електродвигуна ймовірність того, що в даний навмання взятий момент часу він працює дорівнює 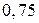. Число 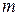одночасно включених електродвигунів може бути 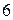, , 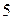, , , , 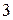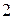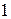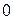. Знайти закон розподілу цієї дискретної випадкової величини 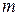– числа одночасно включених електродвигунів. Побудувати многокутник розподілу і знайти найімовірніше число одночасно працюючих електродвигунів.

Розв’язання. За умовою задачі , .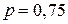

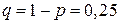Випадкова величина 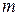– число одночасно включених електродвигунів, може прийняти значення 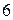, , 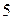, , , , 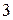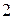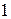з ймовірностями, які ми визначимо за формулою Бернуллі:

; ; ; ; ; ; .

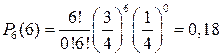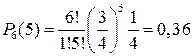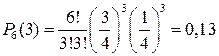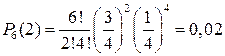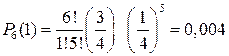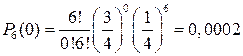Тоді маємо закон (ряд) розподілу

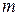
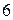
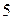
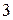
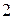
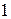
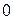
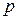
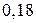
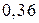
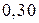
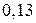
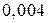
За цією таблицею побудуємо многокутник розподілу.

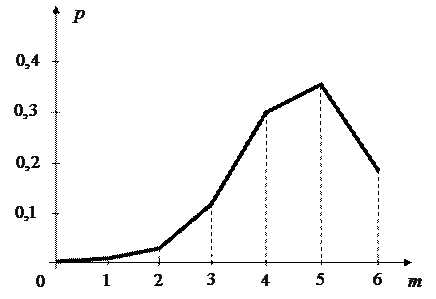
Найімовірніше число можна знайти або з таблиці або з многокутника розподілу. Цим числом є .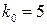

Приклад 4. Що ймовірніше виграти в шахи у рівносильного супротивника (нічиї виключаються):

1) три партії з чотирьох чи п’ять з восьми?

2) Не менше трьох партій з чотирьох чи не менше п’яти партій з восьми.

Розв’язання. За умовою задачі 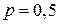, 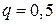. Тоді:

1) за формулою Бернуллі маємо:

;

.

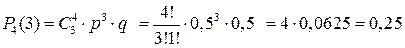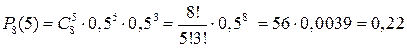Оскільки 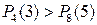, то ймовірніше виграти три партії з чотирьох.

2) Позначимо через 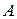подію, що полягає в тому, що можна виграти не менше трьох партій з чотирьох, а через – що можна виграти не менше п’яти партій з восьми, тоді

;

.

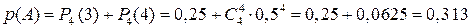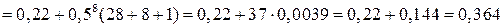Оскільки 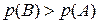, то ймовірніше виграти не менше п’яти партій з восьми ніж три з чотирьох.

Приклад 5. В сім’ї шестеро дітей. Ймовірність народження хлопчика дорівнює 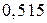, дівчинки – 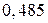. Обчислити ймовірність того, що в сім’ї не більше двох дівчат.

Розв’язання. За умовою задачі 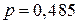, 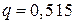. Позначимо через 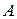подію, що в сім’ї не більше двох дівчат, тоді за теоремою додавання ймовірностей та формулою Бернуллі маємо:

.

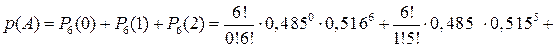
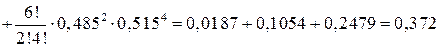Приклад 6. У цеху 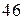верстатів. Для кожного верстата ймовірність того, що він в даний навмання взятий момент часу працює, дорівнює 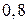. Обчислити найімовірніше число працюючих в даний момент верстатів.

Розв’язання. За умовою задачі 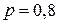, , 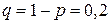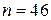. Тоді на підставі нерівності (3):

,

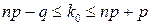маємо

.

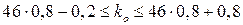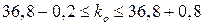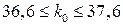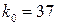; , верстатів.

Приклад 7. Для даного баскетболіста ймовірність закинути м’яча в корзину при кожнім кидку дорівнює 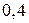. Зроблено 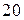кидків. Обчислити найімовірніше число влучень в корзину і відповідну ймовірність.

Розв’язання. За умовою задачі 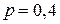, , 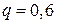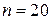. Тоді за формулою (3)

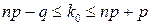
маємо

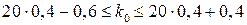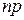, – ціле, тоді 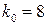кидків.

Відповідну ймовірність обчислимо за формулою Бернуллі:

.

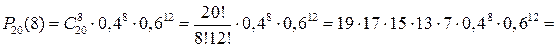
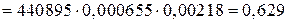Приклад 8. В результаті багаторічних спостережень для деякої місцевості було з’ясовано, що ймовірність випадання дощу протягом дня 1-го вересня дорівнює 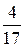. Обчислити найімовірніше число дощових днів 1-го вересня за найближчі наступні 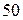років.

Розв’язання. ; ; .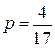

.

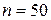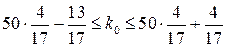
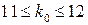Приклад 9. Скільки треба посіяти насіння, схожість якого 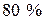, щоб найімовірніше число зернят, яке зійде було .

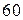Розв’язання. За умовою , , ,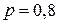

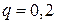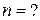
Тоді за формулою (3) маємо:

, ;

, ;

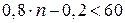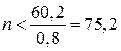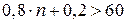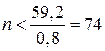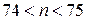(зернят).

Дата добавления: 2014-01-11