Распределения, применяемые при статистическом контроле качества

В курсе «Теории вероятностей и математической статистики» достаточно подробно рассматриваются различные виды распределений как дискретных, так и непрерывных случайных величин. Дискретные распределения моделируют так называемые бинарные события, т.е. события, относительно которых можно сделать заключение о том, что оно имело место или его не было. Такие события называют также альтернативными. Например, при контроле качества в виде наличия раковин или цветов побежалости на поверхности, размеры которых не имеют значения, случайным бинарным событием является только сам факт их наличия или отсутствия. Непрерывные распределения описывают измеримые характеристики носителей качества, которые называются «количественными признаками» и могут принимать любое числовое значение в некотором ограниченном или неограниченном интервале допустимых значений.

При использовании математической статистики в системах контроля и управления процессами следует различать проблемы, связанные с распределением контрольных характеристик на выходе процесса, от проблемы моделирования методов контроля. Когда речь идёт о распределении признаков качества и несоответствий в партиях, то имеют в виду анализ результата работы технологического процесса производства как генератора случайных чисел – показателей качества продукции. При моделировании (статистическом описании) процедур контроля речь идёт о математическом представлении способов получения и обработки информации о характеристиках уже изготовленной продукции, об адекватности и точности контроля как самостоятельного процесса, на выходе которого должны быть сформированы надёжные управляющие решения. Поэтому говорить, например, о распределении какого-то признака качества по гипергеометрическому закону не совсем корректно. Гипергеометрический закон распределения определяет количество несоответствующих изделий, попадающих в выборку, вообще говоря, при любом законе распределения несоответствий в партии, но при условии формирования выборки по правилу «без возвращения» и анализе в ходе контроля только бинарного отношения: «годен – негоден». Гипергеометрическое распределение изначально предполагает процесс взятия выборки, т.е. выполнение процедуры контроля.

Сложнее с биноминальным распределением. Биноминальный закон распределения может описывать выход технологического процесса производства, когда каждое изделие с одинаковой вероятностью может быть как годным, так и негодным. Кроме того, сама процедура выборочного контроля, когда выборка берётся «с возвращением» и анализируется бинарное отношение «годен – негоден», – тоже описывается с помощью биноминального распределения.

Распределение Пуассона может описывать только распределение несоответствий на выходе процесса производства. Использование этого распределения для обработки результатов выборочного контроля делается исключительно с целью упрощения математически сложных формул гипергеометрической и биноминальной моделей процедур контроля.

Нормальный закон распределения может использоваться для упрощения обработки результатов контроля альтернативных признаков качества и описывать закон распределения количественных показателей качества на выходе производственного процесса как генератора непрерывных случайных величин.

2.3.1 Гипергеометрическое распределение.

Наиболее полной и точной моделью, отражающей методику контроля качества для любых бинарных распределений, является следующая:

Предположим, имеется ящик с конечным числом N шаров, D из которых белые, а остальные N - D – черные. Очевидно, что, если изъять из ящика n шаров, т.е. сделать выборку объема n и посчитать количество белых шаров, оказавшихся в выборке, то это количество белых шаров будет зависеть от общего числа шаров в ящике N, числа белых шаров в ящике D и объема выборки. Чтобы выразить это математически, определим вероятность того, что в выборке объема n будет d =1, 2, 3,..., k белых шаров. Из комбинаторики известно, что из всех возможных выборок объема n из общей совокупности объема N можно составить всего С_Nⁿ сочетаний:

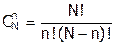, (2.9)

где С_Nⁿ – число возможных наборов по n элементов из множества в N элементов, в которых не учитывается последовательность элементов. С другой стороны каждая такая выборка может содержать С_Dⁿ раз k белых шаров и каждый раз сочетаться с 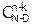случаями, когда остальные шары в каждой выборке будут черными. Следовательно, исходя из классического определения вероятности, получим условное распределение вида:

H(k | N; D; n)=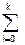hy(i|N; D; n), (2.10)

где = hy(i | N; D; n)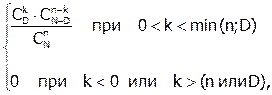

где знак «|» означает «при условии». (В формуле (2.10) автоматически учтено, что в выборку не может попасть более n или более D, белых шаров).

Важно отметить, что формула (2.10) описывает одновременно вероятность того, что если в выборке из n шаров обнаружено k белых шаров, то в ящике с N шарами содержится D белых, т.е. Р(D | N; n; k) эквивалентна вероятности Р(k | N; D; n).

Распределение (2.10) называется гипергеометрическим. Функция этого распределения записывается в виде:

Hy(k | N; D; n)=P(d<k | N; D; n)=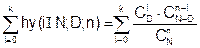 (2.11)

Можно показать, что для гипергеометрического распределения математическое ожидание равно:

M[k = d] = nP, (2.12)

где Р = D/N – доля белых шаров в ящике.

Дисперсия гипергеометрического распределения равна:

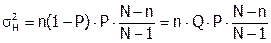, (2.13)

где Q = 1 – P – доля черных шаров в ящике.

Таким образом, гипергеометрическое распределение является четырёхпараметрическим и кроме значения k определяется параметрами N; D и n. Распределение (2.11) с учётом того, что объём партии может достигать нескольких тысяч единиц продукции, является достаточно сложным для расчета даже при использовании современной вычислительной техники.

Дата добавления: 2014-01-15