Распределение Пуассона. Рассмотрим поток событий, т.е

Рассмотрим поток событий, т.е. последовательность событий, которые наступают в случайные моменты времени. Любой производственный процесс можно, в принципе, рассматривать как поток. Например, по конвейеру «течёт» поток изделий, в котором в случайные моменты времени попадаются несоответствующие изделия. В производстве тканей удобно под потоком рассматривать множество натянутых параллельных нитей. При этом случайным событием является обрыв одной из нитей. Тогда независимой переменной потока является геометрическая переменная, связанная с номером нити.

Поток событий называется простым или Пуассоновским, если он подчиняется трем условиям одновременно:

1) условию стационарности: вероятность наступления события в малом отрезке времени Δt пропорциональна величине этого интервала с точностью до бесконечно малой более высокого порядка:

P(d=1) ≈ c·Δt + O(Δt),

где O(Δt) – бесконечно малая величина порядка (Δt)²;

с – некоторая константа.

2) условию ординарности: вероятность наступления в интервале Δt более одного события стремится к нулю быстрее, чем Δt:

;

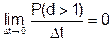3) условию отсутствия последействия: частоты появления событий в непересекающихся интервалах времени независимы, т.е. появление k событий в I -ом интервале Δt_i не зависит от того, с какой частотой появлялись события в предшествующие моменты времени.

Эти условия достаточно жесткие и редко, когда удается строго показать, что они выполняются для реального процесса. Обычно легче показать какое условие не выполняется и при моделировании рассматриваемого процесса потоком Пуассона обязательно оговорить невыполнение этого условия или изменить модельные условия, чтобы сгладить отступление от строгого выполнения всех вышеприведённых условий. Например, для одного станка появление несоответствующего размера детали зависит от износа инструмента и, следовательно, частота появления этого события не будет пропорциональна интервалу времени (будет расти с ростом износа инструмента). Однако, если рассматривать несколько станков со случайными (равномерными) моментами смены инструментов, то применимость простейшего потока для описания появления несоответствий будет вполне оправданной. Применима эта модель и, если под моментами времени Δt полагать интервалы между сменами инструмента. Чаще всего распределение, связанное с простейшим потоком используется как упрощение более точных моделей, описываемых гипергеометрическим или биномиальным распределением.

Распределение, моделирующее простейший поток, подчиняется распределению Пуассона:

Р(d=k) = р₀(d=k | λ)= (2.18)

Это распределение имеет функцию распределения:

P₀(d<k | λ) = 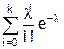(2.19)

При этом единственный параметр этого распределения равен:

λ = n·P

Математическое ожидание и дисперсия этого распределения равны параметру λ:

M[d] = λ = n·P (2.20)

σ_р² = λ = n·P (2.21)

Дата добавления: 2014-01-15