Двухступенчатые планы выборочного контроля для альтернативных признаков качества

При двухступенчатом плане контроля из партии объема N сначала берут выборку объема n₁. Контроль прекращают после проверки изделий первой выборки в двух случаях:

1) если число несоответствующих изделий k₁, не превышает приемочного числа c₁ (k₁ £ c₁), партию принимают;

2) если число несоответствующих изделий k₁ равно или превышает браковочное число d₁ (k₁ ³ d₁), партию бракуют.

В случае c₁ < k₁ < d₁, берут вторую выборку объемом n₂ и партию принимают, если суммарное число несоответствующих изделий в обеих выборках не превышает приемочного числа c₂ (k₁+k₂ £ c₂), при k₁+k₂ > c₂ партию бракуют.

(Составьте схему алгоритма двухступенчатого контроля аналогично схеме по рис. 4.1).

Параметры плана двухступенчатого контроля определяют аналогичным способом, как и при одноступенчатом контроле, т.е. из условия прохождения ОХ через заданные точки (см. (4.2)). Поскольку при двухступенчатом контроле число подлежащих определению параметров равно 5 (n₁, c₁, d₁, n₂, c₂ или d₁), а уравнений всего два, используются дополнительные условия:

c₁ < d₁ – 1 < c₂ < n₁; d₁ – 1 £ c₂ < n₁ + n₂; n₁ = n₂ или n₁ = 2×n₂ и т.п. (см. / /).

В стандартах приведены таблицы допустимых двухступенчатых планов контроля с одинаковым и удвоенным объемом выборки на второй ступени для уровня дефектности партии в виде процента несоответствующих единиц продукции в партии любого объема. После выбора плана выборочного контроля можно построить ОХ, исходя из следующих соображений:

1) вероятность приемки партии есть сумма двух несовместимых событий:

- события А1 = {партия принята по результатам контроля первой ступени};

- события А2 = {партия принята по результатам проверки второй выборки с учетом результатов контроля первой выборки}.

Событие А2 является сложным событием, для осуществления которого необходимо совместное выполнение двух следующих событий:

- события В1 = {число несоответствующих изделий в первой выборке находится в пределах с₁< k₁< d₁};

- события В2 = {суммарное число дефектных изделий в обеих выборках не превышает приемочного числа с₂ (k₁+k₂ £ с₂)}.

Таким образом:

L(q) = P(A1) + P(A2) = P(A1) + P(B1∩B2). (4.3)

Исходя из того, что событие А1 как и при одноступенчатом контроле моделирует гипергеометрический закон распределения числа дефектных изделий в партии (выборка без возвращения), вероятность события А1 будет равна:

P(A1) = P(k₁ £ с₁) = Hy(с₁/;N;Nq;n₁) = .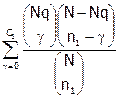

Вероятность события А2 в соответствии с формулой для полной вероятности сложного события можно выразить как сумму по всем возможным значениям k₁= g:

P(A2) = P(В1 Ù В2) = P[(с₁ < k₁ £ d₁) ∩ (k₁ + k₂ £ с₂)] =
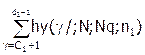= × Hy(с₂ - g/;N-n;Nq-g;n₂).

Окончательно, подставив выражения для Р(А1) и Р(А2) в (4.3), соотношение для ОХ при двухступенчатом плане выборочного контроля можно записать в следующем виде:

L(q)= Hy(c₁/;N;Nq;n₁)+ 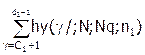· Hy(c₂- g/;N-n;Nq-g;n₂), (4.4)

где hy(g/;N;Nq;n₁)= 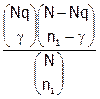- плотность гипергеометрического распределения.

Вычисления по этой формуле представляют определенные трудности. Однако, расчёты существенно упростятся как и в случае одноступенчатого плана контроля при использовании персонального компьютера с установленной на нем прикладной программой «Excel». В этой программе имеется подпрограмма расчета плотности гипергеометрического распределения hy(k/;N;D;n). Функцию гипергеометрического распределения можно рассчитать как сумму:

Hy(c/;N;D;n)= .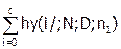

При выполнении соответствующих условий можно использовать приближения:

- биноминальное: L_в(q)=Bi(c₁/;q;n₁)+ 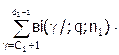Bi(c₂/;q;n₂);

- Пуассона: L_p(q)=Ро(c₁/;n₁;q) +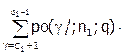Po(c₂- g/; n₂;q).

Дата добавления: 2014-01-15