Планы выборочного контроля при известной дисперсии и одностороннем ограничении признака качества

Рассмотрим принципы построения планов выборочного контроля качества для случая известной дисперсии s² и одностороннем ограничении признака качества, например, когда требование к соответствию изделия задано в виде ограничения на нижнее предельное значение: изделие годное, если показатель качества у ³ а. Качество партии характеризует уровень несоответствий q_п: партия соответствует требования и подлежит поставке потребителю, если доля несоответствующих изделий в ней не превышает заданное (согласованное между поставщиком и потребителем) значение q_o, т.е. если

q_п £ q_o (5.4)

или, в соответствии с (5.2), когда

Ф(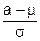) £ q_o. (5.5)

Переходя в (5.5) к квантилям и с учётом монотонности функции стандартного распределения, представим требование к групповому показателю через требование к математическому ожиданию m:

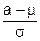£ z_qo или m ³ а + z_1-qo×s. (5.6)

Для оценки неизвестного значения математического ожидания показателя качества m в партии используем достаточную статистику (см. п. 3.4) в виде выборочного среднего:

=,

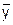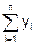где n – объём выборки.

Если для выполнения условия (5.4) относительно математического ожидания необходимо и достаточно выполнения соотношения (5.6), то для выборочного среднего необходимо выполнение более строгого неравенства:

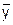³ m + d, (5.7)

где d – доверительный интервал возможных значений m, соответствующих полученному по выборке конкретному значению 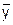, связанный со статической неопределённостью оценки математического ожидания по выборочному среднему.

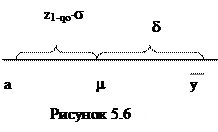Величину d можно определить из уравнения:

Р((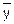 ³ m + d)|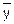) = g, (5.8)

где g – доверительная вероятность того, что значение m окажется больше («левее») значения 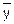- d (см. рисунок 5.6). С учётом «нормальности» распределения признака качества у и соответственно «нормальности» распределения выборочного среднего 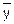с параметрами (m; s/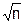), уравнение (5.8) можно представить в виде:

Р((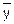≥ m + d)|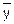) = 1 - 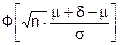= =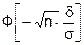 g.

Откуда, переходя к квантилям, можно записать:

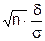= z_1-g или окончательно d = .

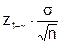Поэтому для выполнения (5.4) из (5.7) с учётом (5.6) для выборочного среднего должно выполняться соотношение:

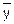³ а + z_1-qo×s + 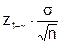= а + s×(z_1-qo + 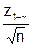) = а + k×s, (5.9)

где k = (z_1-qo + 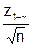) – приёмочный коэффициент, определяющий через исходные параметры плана контроля q_o, n и g такое требование к значению выборочного среднего, чтобы выполнялось соотношение (5.4).

Из (5.9) автоматически получается уравнение для ОХ плана выборочного контроля L(m):

L(m) = P(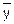³ а + k×s) = 1 - 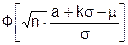= 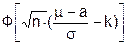. (5.10)

Учитывая (5.2) в квантильной форме, можно получить уравнение для ОХ в виде зависимости вероятности приёмки партии от предполагаемого уровня несоответствий:

L(q) = .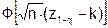

Если теперь записать значения ОХ для q = AQL и q = RQL, то получим систему:

(5.11)

Или, переходя к квантилям:

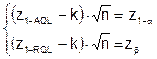
Откуда нетрудно получить:

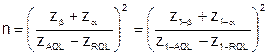(5.12)

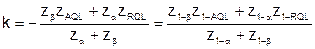(5.13)

Аналогично при ограничении в виде верхнего предельного значения в (изделие годное, если показатель качества у £ в), ограничение на значение выборочного среднего представим в виде:

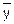£ в - k×s,

где, по-прежнему, k = (z_1-qo + 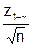) – приёмочный коэффициент плана выборочного контроля.

Тогда, для ОХ можно записать:

L(m) = P(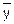£ в - k×s) = = .

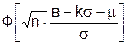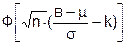Или с учётом (5.1) в квантильной форме:

L(q) = .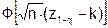

Таким образом, вне зависимости от вида ограничения (верхнего или нижнего) уравнение ОХ и, соответственно, соотношения для определения приёмочного коэффициента k и объёма выборки n получаются идентичными.

Примечание. Если вернуться к (5.9) и сравнить k =(z_1-qo + 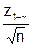) c (5.13), то нетрудно получить:

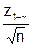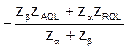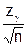(z_1-qo + ) =или: = z_qo .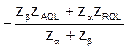

Из последнего равенства, c учётом (5.12), следует:

z_1-g = 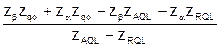. (5.14)

Например, в системе AQL принимают: q_o = AQL. Тогда по (5.14) получаем:

z_1-g = 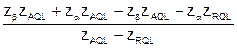= z_a, т.е. g = 1- a.

В системе ПРП: q_o = RQL = NQL и тогда g = b.

Дата добавления: 2014-01-15