Планы выборочного контроля при неизвестной дисперсии и одностороннем ограничении признака качества

Если дисперсия s² заранее неизвестна, то соотношения для уровня несоответствий в партии (5.1) – (5.3) содержат две неизвестные величины и, следовательно, помимо математического ожидания по выборке следует оценить и стандартное отклонение s. В качестве эффективной, несмещённой и асимптотически нормальной оценки для стандартного отклонения используют её выборочное значение:

.

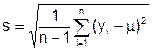Однако, как и в случае с математическим ожиданием непосредственно использовать эту оценку в формулах нельзя. Действительно, известно, что отношение 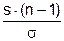подчиняется распределению c² с n-1 степенью свободы. Тогда, например, в случае ограничения показателя качества снизу (изделие годное, если у_i ³ а), аналог аргумента в соотношении (5.2) для уровня несоответствий в партии можно записать в следующем виде:

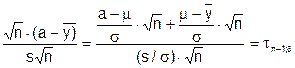, (5.14)

где величина t_n-1;d - имеет нецентральное распределение Стьюдента с n-1 степенью свободы и параметром нецентральности:

d = .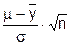

Для получения параметров планов контроля можно непосредственно использовать статистику (5.14), но можно получить и более простое приближение в виде, аналогичном (5.9):

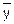≥ а + k×s.

Т.е. партия соответствует требованиям, если случайная величина x = 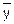- k×s превышает нижнее предельное значение для признака качества а, т.е. если x ³ а. Тогда, используя асимптотическую нормальность выборочного стандартного отклонения s Î no(s;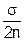), случайную величину x можно считать распределённой по нормальному закону с параметрами:

М[x] = m - k×s и D[x] = =.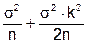

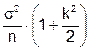Поэтому ОХ для случая одностороннего нижнего ограничения при неизвестной дисперсии можно представить в виде;

L(m) = P(x ³ а) = 1 - Ф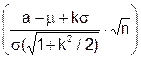или

L(q) = Ф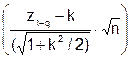. (5.15)

Примечание. В литературе / / предлагается более точная формула:

L(q) = Ф.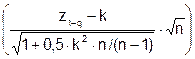

Если теперь как и в случае известной дисперсии считать, что ОХ, вычисляемая по формуле (5.15), должна проходить через точки с координатами (q = AQL; 1-a) и (q = RQL; b), то нетрудно получить выражения для приёмочного коэффициента и объёма выборки (Получите!):

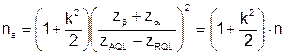; (5.16)

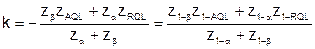. (5.17)

Естественно, точно такие же соотношения получаются и в случае неизвестной дисперсии и одностороннем верхнем ограничении признака качества (изделие годное, если показатель качества у £ b). Таким образом, при неизвестной дисперсии и любом одностороннем ограничении признака качества приёмочные коэффициенты такие же, как и при известной дисперсии, а объём выборки при прочих равных условиях в случае неизвестной дисперсии будет в 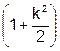раз больше, чем в случае, когда дисперсия известна.

Дата добавления: 2014-01-15