
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила принятия решений на основе толерантных границ (по ГОСТ Р 50779.50)
|
|
|
|
Связь доверительной вероятности интервальной оценки уровня несоответствий контролируемой партии продукции с доверительной вероятностью оценок параметров функции распределения количественного показателя качества.
Планы выборочного контроля по количественному признаку в системе ПРП
Одним из основных положений математической статистики, на которых базируются принципы расчета параметров планов выборочного контроля по ГОСТ Р 50779.50 и ГОСТ Р 50779.53 является связь доверительной вероятности интервальной оценки уровня несоответствий * контролируемой партии продукции с доверительной вероятностью оценок параметров функции распределения количественного показателя качества. Именно эта связь позволяет по выборке определять с заданной вероятностью верхнюю доверительную границу qв уровня несоответствий в партии при контроле у поставщика или нижнюю доверительную границу qн при контроле у потребителя. При этом уровни доверия задаются в договоре или иной нормативно-технической документации в виде риска потребителя b для планов контроля у поставщика и в виде риска поставщика a для планов контроля у потребителя. По-видимому, эта связь, констатация которой представлена в приложении Б ГОСТ Р 50779.50, является "темным" местом даже для наиболее эрудированной части инженерно-технического персонала предприятий (испытателей, конструкторов и технологов), не говоря уже о других специалистах и большей части руководителей, не особенно искушенных в тонкостях математической статистики, и поэтому воспринимающих тексты типа упомянутого приложения не просто как непонятный, а потому бессмысленный набор иероглифов, но и подчас как попытку “скрытого вредительства” с помощью неких дьявольских магических заклинаний на вверенном им участке производства.
Итак, действительно, почему же доверительные вероятности уровня несоответствий в партии и оценок параметров функции распределения показателя качества совпадают? Наиболее просто это можно показать для случая нормального распределения показателя качества со стабильной и, следовательно, известной дисперсией. Партия считается годной, если с вероятностью не менее 1-b выполняется условие:
qв £ NQL, (6.1)
где qв – верхняя доверительная граница уровня несоответствий в партии, вычисляемая по (5.3), но с заменой m на ее верхнюю mв или нижнюю mн доверительные границы, оцениваемые по выборке (при известном значении дисперсии s2):
 , при , при 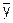 < y* < y*
| (6.2) |
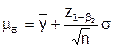 , при , при 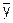 ≥ y* ≥ y*
|
где n – объём выборки;
 – середина поля допуска количественного показателя качества;
– середина поля допуска количественного показателя качества;
zр – квантиль стандартного нормального распределения уровня р причем:
b1 = Р((m < mн)|(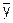 < y*)) и b2 = Р((m > mв)|(
< y*)) и b2 = Р((m > mв)|(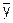 ≥ y*)), (6.3)
≥ y*)), (6.3)
где Р(А|В) – вероятность события А при условии выполнения события B.
Суть замены точечной оценки уровня качества партии на интервальную показана на рисунке 6.1, где представлены графики плотности распределения признака качества для  (график 1, отражающий случай точечной оценки уровня несоответствий) и для m º mв и m º mн (графики 2 и 3 соответственно, представляющие случай интервальной оценки уровня несоответствий). Доля дефектных изделий в партии для всех трех графиков равна площади под соответствующей кривой в области вне отрезка [ a, b].
(график 1, отражающий случай точечной оценки уровня несоответствий) и для m º mв и m º mн (графики 2 и 3 соответственно, представляющие случай интервальной оценки уровня несоответствий). Доля дефектных изделий в партии для всех трех графиков равна площади под соответствующей кривой в области вне отрезка [ a, b].

Рисунок 6.1
Таким образом, интервальная оценка уровня несоответствий в партии всегда односторонняя, тогда как интервальная оценка математического ожидания показателя качества партии может быть односторонней при одностороннем ограничении показателя качества или двусторонней при двустороннем ограничении показателя качества. При этом правило принятия решения по-прежнему соответствует рисунку 5.3.
Можно показать (см., например, /4/), что:

| т.е. qв возрастающая функция от 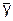 при при 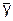 ≥ y* ≥ y*
| (6.4) |
т.е. qв убывающая функция от 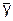 при при 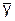 < y*, < y*,
|
Поэтому верхнюю границу qв по результатам выборочного контроля у поставщика следует вычислять по формуле:
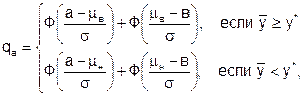
| (6.5) |
полностью совпадающей с формулой из примера 1 приложения Г ГОСТ Р 50779.50, если учесть, что 1-Ф(z)=Ф(-z).
Остается определить, какие уровни доверия 1- b1 и 1- b2, используемые при вычислении mв и mн по (6.2), обеспечат заданный риск потребителя при контроле у поставщика b. Учитывая, что уровень несоответствий в партии qв является монотонно возрастающей функцией от 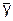 при
при  и монотонно убывающей при
и монотонно убывающей при 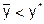 , легко установить, что при получении по результатам выборочного контроля qв < NQL, выполнение неравенства q > NQL автоматически означает, что q > qв, а это возможно только при выполнении события m > mв, если
, легко установить, что при получении по результатам выборочного контроля qв < NQL, выполнение неравенства q > NQL автоматически означает, что q > qв, а это возможно только при выполнении события m > mв, если  , или m < mн, если
, или m < mн, если 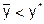 (см. (6.4) и рисунок 6.1). Принимая во внимание независимость события, заключающегося в попадании выборочного среднего
(см. (6.4) и рисунок 6.1). Принимая во внимание независимость события, заключающегося в попадании выборочного среднего 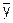 в любую половину допуска [ а, b], на основании теоремы о сумме вероятностей двух независимых событий, можно записать:
в любую половину допуска [ а, b], на основании теоремы о сумме вероятностей двух независимых событий, можно записать:
Р((q > qв)|(qв £ NQL)) = Р((m < mн)|(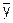 < y*)) + Р((m > mв)|(
< y*)) + Р((m > mв)|(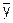 ≥ y*)),
≥ y*)),
или с учётом (6.3):
b = 1 - g = b1 + b2, (6.6)
где g - уровень доверия, используемый при построении доверительного интервала уровня несоответствий по результатам контроля поставщика.
Таким образом, вероятности накрытия истинных значений уровня несоответствий q и математического ожидания m соответствующими доверительными интервалами будут эквивалентны:
Р(q £ qв) = Р(mн|(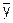 < y*) £ m £ mв|(
< y*) £ m £ mв|(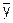 ≥ y*)) = 1 - b = 1 – (b1+b2), (6.7)
≥ y*)) = 1 - b = 1 – (b1+b2), (6.7)
Из соотношения (6.7) вытекает важное следствие:
контроль группового показателя качества можно свести к проверке статистической гипотезы о попадании математического ожидания показателя качества m в доверительный интервал с уровнем значимости 1-b, что с практической точки зрения означает проверку попадания выборочного среднего 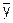 между нижней (НПГ) и верхней (ВПГ) предельных границ, которые можно рассчитать или выбрать из соответствующих таблиц стандарта (см. ГОСТ Р 50779.53) до проведения контроля и установить в технических условиях или в иной нормативно-технической документации.
между нижней (НПГ) и верхней (ВПГ) предельных границ, которые можно рассчитать или выбрать из соответствующих таблиц стандарта (см. ГОСТ Р 50779.53) до проведения контроля и установить в технических условиях или в иной нормативно-технической документации.
Для случая одностороннего ограничения показателя качества можно принять:
1) при заданном только верхнем предельном значении показателя качества (изделие годное при уi £ b):
а = -¥, и, следовательно, всегда 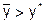 и b1 = Р(m < mн) = 0;
и b1 = Р(m < mн) = 0;
2) при заданном только нижнем предельном значении (изделие годное при уi ≥ а):
b = +¥, и, следовательно, всегда 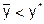 и b2 = Р(m > mв) = 0.
и b2 = Р(m > mв) = 0.
Поэтому, в этом случае, согласно (6.7), mн и mв в (6.3) должны определяться с доверительной вероятностью 1-b.
При двустороннем ограничении показателя качества согласно (6.6) и (6.7) существует возможность установки различных значений b1 и b2, естественно, при соблюдении условия b1 + b2 = b. По-видимому, при расчёте параметров планов выборочного контроля следует использовать равные значения b1 = b2 = b/2. Только в этом случае при проверке гипотезы о попадании математического ожидания в доверительный интервал по значению выборочного среднего будет обеспечиваться наиболее мощный несмещённый критерий, который доминирует все другие критерии с b1 ¹ b2. С точки зрения стандартизации концепции ПРП это означает, что значения НПГ и ВПГ в табл. 4 – 8 и 11 ГОСТ Р 50779.53 должны иметь разные значения для случаев одностороннего и двустороннего ограничения показателя качества. Тогда применение параметров таких планов контроля (с b1 = b2 = b/2) для любых планов с b1 ¹ b2 будет заведомо допустимым в соответствии с п. 5.3 ГОСТ Р 50779.30, т.е. оперативная характеристика (ОХ) плана с b1 = b2 в точке с абсциссой q = NQL пройдёт выше, чем ОХ любого плана с b1 ¹ b2 при прочих равных условиях. Если не придерживаться этого правила, то возможны недоразумения. В качестве примера можно привести построение таблиц 4 – 8 и 11 ГОСТ Р50779.53, содержащих значения коэффициентов К1 и К2 для определения нижних и верхних приемочных границ для 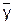 . Очевидно, что значения коэффициентов в этих таблицах получены по формуле (5.9):
. Очевидно, что значения коэффициентов в этих таблицах получены по формуле (5.9):
K1 = z1-NQL+ - для планов контроля поставщика (см. табл. 4 - 8 ГОСТ Р50779.53);
- для планов контроля поставщика (см. табл. 4 - 8 ГОСТ Р50779.53);
K2 = z1-NQL-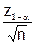 - для планов контроля потребителя (см. табл. 11 ГОСТ Р 50779.53).
- для планов контроля потребителя (см. табл. 11 ГОСТ Р 50779.53).
Не вызывает сомнения правильность этих значений для случая одностороннего ограничения показателя качества (изделие годное, если yi ³ a или если yi £ b). Однако, при двустороннем допуске (изделие годное, если а £ y £ b) эти таблицы пригодны только для частного случая, когда для каждого предельного значения показателя качества задаётся отдельное значение уровня несоответствий NQL.
В самом деле, если в примере Б1 приложения Б ГОСТ Р 50779.53 значение NQL = 4 % относится ко всем изделиям с диаметром вне поля допуска, а в результате выборочного контроля этого размера выборочное среднее окажется равным нижней приёмочной границе, т.е. 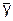 = НПГ = а + К1s, то в соответствии с ГОСТ Р 50779.53 партию можно считать годной. Однако, в соответствии с ГОСТ Р 50779.50:
= НПГ = а + К1s, то в соответствии с ГОСТ Р 50779.53 партию можно считать годной. Однако, в соответствии с ГОСТ Р 50779.50:

где К1 = 1,75 и b = 0,5 (см. пример по п.Б1 Приложения Б ГОСТ Р 50779.53).
Следовательно, по ГОСТ Р 50779.50 получается, что qв > NQL (даже без учета Ф2) и, поэтому, партию в этом случае нельзя принять, что противоречит решению по ГОСТ Р 50779.53.
Таким образом, применение правила приемки (6.1) с обеспечением риска потребителя при контроле у поставщика не более заданного значения b предполагает определение mн или mв в (6.2) с доверительной вероятностью
1-b1 = 1-b2 = 1-b/2 при двустороннем ограничении показателя качества и 1-b при любом одностороннем ограничении, т.е. mв и mн следует вычислять по формулам:
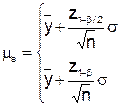
| при двустороннем ограничении показателя качества; |
| при любом одностороннем ограничении показателя качества; | |
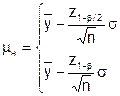
| при двустороннем ограничении показателя качества; |
| при любом одностороннем ограничении показателя качества. |
Кстати, планы контроля с несимметричными уровнями значимости (b1 ¹ b2) вполне могут найти применение. Например, для плана контроля качества толщины слоя покрытия d можно установить разные значения рисков:
b1 = Р((md < mdн)| (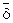 < d*)) < b2 = Р((md > mdв)| (
< d*)) < b2 = Р((md > mdв)| (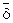 ≥ d*)),
≥ d*)),
поскольку именно первый риск в большей степени «определяет» качество деталей с покрытием, чем второй, который необходим, прежде всего, для обеспечения экономии материала покрытия. Т.е. при заданных параметрах плана контроля (NQL, b = b1 + b2) среди несоответствующих деталей с двусторонним ограничением на толщину покрытия вероятность обнаружить деталь с d > в вполне может быть выше, чем вероятность обнаружить деталь с d < а. Такой подход представляется более разумным, чем назначение на нижнее и верхнее предельные значения толщины покрытия (как для односторонних) разных значений уровня несоответствий и риска, как это предлагается в ГОСТ Р 50779.74 (система AQL).
Аналогичные рассуждения для плана контроля у потребителя с правилом принятия решения в виде условия: партия не соответствует требованиям по качеству в случае выполнения условия:
qн > NQL, (6.8)
где qн – нижняя граница доверительного интервала уровня несоответствий в партии, рассчитываемая по результатам выборочного контроля по формуле:

| (6.9) |
приводят к необходимости для обеспечения риска поставщика не менее заданного значения a определять mн и mв в (6.9) с доверительной вероятностью 1-a/2 в случае двустороннего ограничения показателя качества и 1-a в случае любого одностороннего ограничения:

| при двустороннем ограничении показателя качества; |
| при любом одностороннем ограничении показателя качества; | |
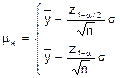
| при двустороннем ограничении показателя качества; |
| при любом одностороннем ограничении показателя качества. |
6.2 Предельное значение  при приёмочном контроле качества по стандартам концепции ПРП.
при приёмочном контроле качества по стандартам концепции ПРП.
Представленный в предыдущем разделе теоретический подход к приёмочному контролю качества на основе соотношения (6.1) позволяет, в частности, корректно оценить минимально допустимое значение отношения поля допуска показателя качества D = b – а к стабильному и, следовательно, известному значению стандартного отклонения s. Т.е. уточнить предельное значение отношения  (где, по-прежнему, а и b – предельные значения показателя качества у: изделие годное, если а £ yi £ b), которое допускает контроль установленного значения уровня несоответствий NQL выборочными методами. В табл. 2 ГОСТ Р 50779.53 приведен вариант предельных значений этого отношения без каких-либо указаний о том, каким образом эти значения получены. При этом подчеркнуто, что для меньших значений
(где, по-прежнему, а и b – предельные значения показателя качества у: изделие годное, если а £ yi £ b), которое допускает контроль установленного значения уровня несоответствий NQL выборочными методами. В табл. 2 ГОСТ Р 50779.53 приведен вариант предельных значений этого отношения без каких-либо указаний о том, каким образом эти значения получены. При этом подчеркнуто, что для меньших значений  , соответствующее значение NQL "может быть подтверждено практически только сплошным контролем поставщика" (см. примечание к п. 3.7 ГОСТ Р 50779.53). Это утверждение не согласуется с данным из таблиц А7 - А11 приложения А ГОСТ Р 50779.53. В самом деле, если поставщик, используя соответствующие методы управления качеством (в том числе и средства SPC), предполагает, что математическое ожидание показателя качества изготовленных партий продукции принимает значение максимально близкое к середине поля допуска:
, соответствующее значение NQL "может быть подтверждено практически только сплошным контролем поставщика" (см. примечание к п. 3.7 ГОСТ Р 50779.53). Это утверждение не согласуется с данным из таблиц А7 - А11 приложения А ГОСТ Р 50779.53. В самом деле, если поставщик, используя соответствующие методы управления качеством (в том числе и средства SPC), предполагает, что математическое ожидание показателя качества изготовленных партий продукции принимает значение максимально близкое к середине поля допуска: 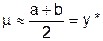 . Тогда предполагаемый запас качества g по табл. А1 оказывается равным половине предельных значений по табл. 2 ГОСТ Р 50779.53:
. Тогда предполагаемый запас качества g по табл. А1 оказывается равным половине предельных значений по табл. 2 ГОСТ Р 50779.53:
g =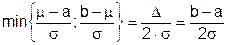 .
.
Казалось бы, предельные значения по табл. 2 ГОСТ Р 50779.53 не должны превышать удвоенных значений предполагаемого запаса качества по таблицам приложения А для любых, по крайней мере, приведенных в этом приложении объемов выборки (до n = 200). Однако, согласно табл. А7 (β = 0,1), выборочный приемочный контроль поставщика обеспечивает приемку партий с вероятностью не менее 0,95, например, для NQL = 0,15 % и n = 40 при отношении  = 6,96, т.е. при меньшем значении, чем
= 6,96, т.е. при меньшем значении, чем  = 7, приведенном в табл. 2 (для более высоких значений β и объёмов выборки n использование выборочных методов контроля оказывается возможным и при меньших значениях отношения
= 7, приведенном в табл. 2 (для более высоких значений β и объёмов выборки n использование выборочных методов контроля оказывается возможным и при меньших значениях отношения  ).
).
Не имея представления как рассчитаны значения в табл. 2 ГОСТ Р 50779.53, предлагаем свой способ получения предельных значений  . Известно (см., п. 5.3.4), что минимальный уровень несоответствий, который может быть обеспечен при двустороннем ограничении нормально распределенного показателя качества определяется по формуле:
. Известно (см., п. 5.3.4), что минимальный уровень несоответствий, который может быть обеспечен при двустороннем ограничении нормально распределенного показателя качества определяется по формуле:
 , (6.10)
, (6.10)
которая получается при среднем значении показателя качества партии в точности равном середине поля допуска, т.е. при m = y*. При выборочном контроле выборочное среднее  с доверительной вероятностью 2×h может попасть в интервал:
с доверительной вероятностью 2×h может попасть в интервал:
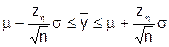 .
.
Удобно связать этот доверительный интервал с собственным риском поставщика при контроле поставщика a*, тогда:
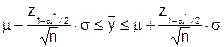
или, учитывая, что для минимального фактического уровня несоответствий qmin по (6.10) необходимо выполнение равенства: m = y*, можно записать:
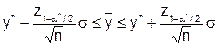 , (6.11)
, (6.11)
где a*= 0,05 - 0,1 – рекомендуемые значения собственного риска стороны, выполняющей контроль (см. ГОСТ Р50779.50).
Формула (6.11) отражает тот факт, что даже, если в идеальном случае с целью обеспечения qmin поставщику удаётся поддерживать свой технологический процесс таким образом, чтобы выполнялось условие m» y*, всё равно в силу неопределённости из-за использования выборочных методов контроля, значение выборочного среднего 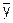 с вероятностью 1-a* будет попадать в интервал [
с вероятностью 1-a* будет попадать в интервал [ ,
, ].
].
Кроме того, поскольку для принятия решения о соответствии или несоответствии партии, с NQL необходимо сравнивать верхнюю границу уровня несоответствий в партии qв, следует учесть возможность дополнительного отклонения выборочного среднего 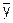 от y*, связанную обеспечением риска потребителя при контроле поставщика (см. п. 6.1):
от y*, связанную обеспечением риска потребителя при контроле поставщика (см. п. 6.1):
 (6.12)
(6.12)
где g* = 1- b/2 – уровень доверия, обеспечивающий риск потребителя при контроле поставщика не более b.
В силу симметричности расположения интервальных оценок математического ожидания признака качества партии mн и mвотносительно y*, достаточно рассмотреть случай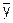 < y* (случай
< y* (случай  приводит к аналогичным результатам).
приводит к аналогичным результатам).
С учётом (6.12) доли изделий с показателями качества меньше нижней границы допуска Ф1 и больше верхней границы допуска Ф2 (см. соотношения (6.5)) можно представить в виде:
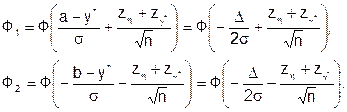 (6.13)
(6.13)
Таким образом, предельно - минимальное значение 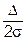 для любого заданного NQL = qв будет соответствовать равенству:
для любого заданного NQL = qв будет соответствовать равенству:
 (6.14)
(6.14)
Представим (6.14) в виде:
NQL = c1×NQL + c2×NQL,
где c1 + c2 = 1 (с1 и с2 – неслучайные множители такие, что Ф1 = с1×NQL и Ф2 = с2×NQL).
Тогда можно записать:

Или, переходя к квантилям:
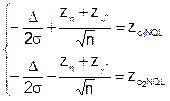 (6.15)
(6.15)
Складывая и вычитая почленно уравнения системы (6.15), получим:
 (6.16)
(6.16)
Рассматривая систему (6.16), легко установить, что:
1) в силу монотонности обратной (квантильной) функции нормального стандартного распределения второе уравнение системы (6.16) дает единственное решение относительно с1 и с2(с учетом с1+ с2=1);
2) определив с1 и с2 из второго уравнения системы (6.16), можно рассчитать по первому уравнению предельное значение  для любого значения NQL;
для любого значения NQL;
3) предельное значение  зависит от значения комплекса
зависит от значения комплекса  , т.е. от принятых доверительных вероятностей ηи g * и от объема выборки n. Причем при любых значениях ηи g * этот комплекс стремится к 0 при n→ ∞,т.е. в пределе (приn = ∞), zc1×NQL - zc2×NQL= 0 или c1 = c2 = 0,5. В этом случае значение
, т.е. от принятых доверительных вероятностей ηи g * и от объема выборки n. Причем при любых значениях ηи g * этот комплекс стремится к 0 при n→ ∞,т.е. в пределе (приn = ∞), zc1×NQL - zc2×NQL= 0 или c1 = c2 = 0,5. В этом случае значение  будет равно:
будет равно:
 = 2×z1-NQL/2 =
= 2×z1-NQL/2 =  , (6.17)
, (6.17)
что соответствует (5.32) при qmin = NQL. Нетрудно проверить, что в табл. IVs ГОСТ Р 50779.74 значения fs равны обратным значениям по (6.17), т.е. fs =1/ . Очевидно, что при любых значениях h, g* и n, значение
. Очевидно, что при любых значениях h, g* и n, значение  не может быть меньше (
не может быть меньше ( )min.
)min.
Зависимость  от g* и n обусловлена неопределенностью результатов контроля статистическими методами и поэтому в соответствии с ПРП, эту неопределенность следует отнести в пользу второй стороны, т.е. потребителя при контроле у поставщика. По ГОСТ Р 50779.50 максимальное значение g * соответствует значению риска потребителя β = 0,1. Максимальный (табличный) объем выборки по ГОСТ Р50779.53 составляет n = 200. При этих значениях n, g* и a* = 0,05 левая часть второго уравнения системы (6.16) будет равна:
от g* и n обусловлена неопределенностью результатов контроля статистическими методами и поэтому в соответствии с ПРП, эту неопределенность следует отнести в пользу второй стороны, т.е. потребителя при контроле у поставщика. По ГОСТ Р 50779.50 максимальное значение g * соответствует значению риска потребителя β = 0,1. Максимальный (табличный) объем выборки по ГОСТ Р50779.53 составляет n = 200. При этих значениях n, g* и a* = 0,05 левая часть второго уравнения системы (6.16) будет равна:
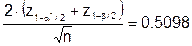 .
.
В таблице 6.1 представлены рассчитанные для этого случая значения с1 и с2 и предельные значения  , соответствующие значениям NQL из ряда по ГОСТ Р 50779.53. Там же приведены значения (
, соответствующие значениям NQL из ряда по ГОСТ Р 50779.53. Там же приведены значения ( )min по (6.17) и значения "хвостов" Ф1, Ф2.
)min по (6.17) и значения "хвостов" Ф1, Ф2.
Таблица 6.1
| NQL,% | D/s* | (D/s)min | D/s | с1 | с2 | Ф1 | Ф2 | qв=Ф1+Ф2 | Ф2/NQL,% |
| 0,15 | 7,0 | 6,3493 | 6,5389 | 0,8584 | 0,1416 | 0,001288 | 0,000212 | 0,0015 | 14,1 |
| 0,25 | 6,5 | 6,0466 | 6,2287 | 0,8493 | 0,1507 | 0,002123 | 0,000377 | 0,0025 | 15,1 |
| 0,4 | 6,2 | 5,7563 | 5,9308 | 0,8399 | 0,1601 | 0,003359 | 0,000641 | 0,004 | 16,0 |
| 0,65 | 5,8 | 5,4429 | 5,6092 | 0,8294 | 0,1706 | 0,005391 | 0,001109 | 0,0065 | 17,1 |
| 1,0 | 5,5 | 5,1517 | 5,3102 | 0,8193 | 0,1807 | 0,008193 | 0,001807 | 0,01 | 18,1 |
| 1,5 | 5,3 | 4,8648 | 5,0156 | 0,8089 | 0,1911 | 0,01213 | 0,002867 | 0,015 | 19,1 |
| 2,5 | 4,8 | 4,4828 | 4,6230 | 0,7945 | 0,2055 | 0,01986 | 0,005138 | 0,025 | 20,6 |
| 4,0 | 4,5 | 4,1075 | 4,2370 | 0,7797 | 0,2203 | 0,03119 | 0,008812 | 0,04 | 22,0 |
| 6,5 | 4,1 | 3,6905 | 3,8079 | 0,7626 | 0,2374 | 0,04957 | 0,01543 | 0,065 | 23,7 |
| 3,6 | 3,2897 | 3,3951 | 0,7456 | 0,2544 | 0,07456 | 0,02544 | 0,1 | 25,4 | |
| 3,3 | 2,8791 | 2,9719 | 0,7276 | 0,2724 | 0,10915 | 0,04085 | 0,15 | 27,2 | |
| 2,7 | 2,3007 | 2,3755 | 0,7018 | 0,2982 | 0,17544 | 0,07456 | 0,25 | 29,8 | |
| Примечание.* По таблице 2 ГОСТ Р 50779.53 |
Из представленного анализа следует, что:
1) минимально-допустимые значения отношения  при организации приёмочного контроля качества в рамках концепции ПРП в отличие от системы AQL зависят не только от уровня несоответствий в партии, но и от объёма выборки n и значений рисков a*, b;
при организации приёмочного контроля качества в рамках концепции ПРП в отличие от системы AQL зависят не только от уровня несоответствий в партии, но и от объёма выборки n и значений рисков a*, b;
2) при увеличении объёма выборки предельные значения  стремятся к обратным значениям коэффициентов fs, представленных в табл. IV ГОСТ Р 50779.74. По-видимому, именно эти значения можно принять в качестве действительно предельных значений, допускающих приёмочный контроль качества выборочными методами, в том числе и в рамках ПРП;
стремятся к обратным значениям коэффициентов fs, представленных в табл. IV ГОСТ Р 50779.74. По-видимому, именно эти значения можно принять в качестве действительно предельных значений, допускающих приёмочный контроль качества выборочными методами, в том числе и в рамках ПРП;
3) расчётные значения параметров планов выборочного контроля неизбежно будут зависеть и от конкретного значения  ;
;
4) в случае реальных значений  , близких к предельным, при расчёте параметров планов контроля следует учитывать оба «хвоста» распределения за пределами поля допуска.
, близких к предельным, при расчёте параметров планов контроля следует учитывать оба «хвоста» распределения за пределами поля допуска.
Согласно общему определению толерантных границ (см., ГОСТ Р 50779.10 и п. 3.2), толерантными называются верхняя xв и нижняя xн границы интервала значений случайной величины Y, внутри которых с заданной вероятностью g заключена не менее, чем доля qг всей генеральной совокупности:
Р { P (xн ≤ Y ≤ xв) ≥ qг } = g. (6.17)
Применительно к методам статистического контроля качества это определение удобно несколько видоизменить. Под толерантными границами количественного признака качества будем понимать такие случайные значения показателя качества xв и xн, зависящие от результатов выборочного контроля, функции и параметров распределения признака качества, в пределах которых с вероятностью не менее 1-b заключены значения признака качества доли, равной 1-NQL от всех изделий в партии:
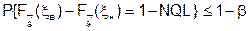 (6.18)
(6.18)
где  - функция распределения значений показателя качества с вектором параметров распределения
- функция распределения значений показателя качества с вектором параметров распределения 
В (6.18) по сравнению с (6.17) переставлены местами знаки равенства и неравенства, поскольку в соответствии с общими положениями (см. ГОСТ Р 50779.30-95) нормативное значение уровня несоответствий NQL строго задается в технических условиях или в договоре, а риск потребителя при контроле поставщика должен быть ограничен сверху значением b. Для планов контроля потребителя аналогичное выражение будет выглядеть следующим образом:
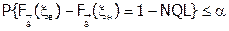 .
.
Чтобы найти доверительные вероятности определения значений случайных величин xв и xн, представим (6.18) в виде условной вероятности:
Рв {xн < y< xв} = 1 - b,
где событие В: 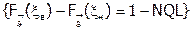 .
.
Обозначив g1 = Рв(yi > xн) и g2 = Рв(yi < xв) – доверительные вероятности определения xв и xн, можно записать, считая события выхода yi за границу xв или xн независимыми:
Рв {yi < xн} + Рв {yi > xв} = b
или
b = 1 - g1 +1 - g2 = 2 – (g1 + g2) = 1 - g. (6.19)
Сравнивая (6.19) с (6.7), легко установить эквивалентность вероятностей:
Р(q £ qв) º P(mн £ m £ mв) º Рв(xн £ y £ xв) = (g1 + g2) - 1 = g = 1 - b. (6.20)
Откуда следует, что при нормальной функции распределения признака качества со стабильной (известной) дисперсией s2 для обеспечения доверительной вероятности g = 1 - b при использовании правила приёмки партии по (6.1) у поставщика или по (6.8) у потребителя толерантные границы xн и xв должны удовлетворять соотношению:
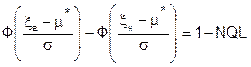 , (6.21)
, (6.21)
где m* - интервальная оценка среднего значения признака качества, определяемая по выборке (см. п.6.1):
а) для плана поставщика:

б) для плана потребителя:

К тому же самому соотношению можно придти и несколько другим путем. Используя непосредственно соотношение (6.5) при qв = NQL, граничные значения признака качества b = xв и a = xн, в пределах которых заключены значения доли 1- NQL годных изделий. В соответствии с (6.18) эти предельные значения и будут толерантными границами, если выполняется равенство:
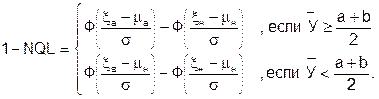
Откуда непосредственно следует (6.21).
Аналогичным образом можно получить связь расчетных соотношений методов толерантных и доверительных границ для плана потребителя.
Соотношение (6.20) приводит к двум важным выводам:
1) возможность проверки соответствия группового показателя качества партии установленным требованиям по значениям толерантных границ: партия соответствует требованиям, если обе толерантные границы находятся в пределах поля допуска (xв ≤ b и (или) xн ≥ a);
2) методы доверительных интервалов и толерантных границ при контроле качества по количественным признакам в рамках концепции ПРП (см. ГОСТ Р 50779.50) – эквивалентны, т.е. приодних и тех же исходных данных приводят к одним и тем же результатам.
Соотношение (6.21) представляет собой одно уравнение с двумя неизвестными (xв и xн). Для его решения необходимо дополнительное условие. Например, при одностороннем ограничении признака качества (изделие годное, если у ³ а или, если у ≤ b) можно принять в =+∞, если задано только а, или а = -∞, если задано только b. Тогда с доверительной вероятностью равной 1 соответствующая толерантная граница так же будет равняться +∞ или -∞. Для плана поставщика при заданной только нижней границе признака качества а, можно принять: xв = +¥. Поэтому из (6.21) следует:

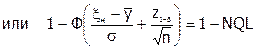 .
.
Откуда легко получить:
 =
= 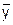 - k×s,
- k×s,
где k = 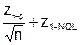 - приёмочный коэффициент, зависящий только от исходных данных плана контроля (сравни с (5.9)).
- приёмочный коэффициент, зависящий только от исходных данных плана контроля (сравни с (5.9)).
Таким образом, получена формула, позволяющая по выборке с установленной достоверностью принимать решение о соответствии или несоответствии партии требованиям к её групповому показателю качества с помощью толерантной границы (см. пример 2 приложения Г ГОСТ Р 50779.50-95): партия соответствует требованиям к её групповому показателю качества, если толерантная граница не выходит за предельное значение признака качества.
Легко показать, что в случае задания верхней границы признака качества в, верхнюю толерантную границу можно определить по формуле:
 =
=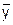 + k×s.
+ k×s.
Аналогично, для планов потребителя можно получить:
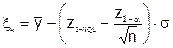 , при заданном только а;
, при заданном только а;
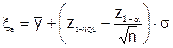 , при заданном только b.
, при заданном только b.
Гораздо сложнее расчет толерантных границ при задании обоих предельных значений признака качества (изделие годное, если а ≤ yi ≤ b). Обычно, в этом случае в качестве дополнительного условия используют условие симметричности:
 ;
;
 ,
,
где ℓ - множитель, имеющий одно и то же значение для xн и xв.
Тогда соотношение (6.21) будет представлять собой уравнение с одним неизвестным (ℓ):
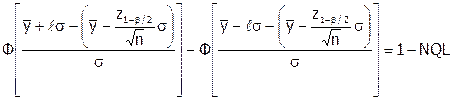 ,
,
которое после несложных преобразований можно записать в следующим виде:
 . (6.22)
. (6.22)
Решить (6.22) можно численными методами. В справочниках по статистике приведены таблицы значений множителей ℓ, удовлетворяющих уравнению (6.22), но для весьма ограниченных значений параметров b и NQL. Кроме того, следует учитывать, что при определении толерантных границ с использованием допущения о симметричности теряется эквивалентность методов толерантных и доверительных границ. В самом деле, в этом случае выполнение одного из условий xн < a или xв > b еще не означает превышения уровня несоответствий партии заданного значения NQL. Проще всего это можно продемонстрировать графически. На рисунке 6.2 представлен случай выхода нижней толерантной границы за пределы нижнего предельного значения признака качества а. Очевидно, что партию можно браковать только при условии, если площадь S1 превышает площадь S2. Иными словами, использование в этом случае правила принятия решения о несоответствии по ГОСТ Р 50779.50-95 приводит к неконтролируемому увеличению риска стороны, производящей контроль, что в ряде случаев крайне нежелательно.
Естественно, существуют способы расчета xн и xв при двустороннем ограничении признака качества с сохранением эквивалентности методов толерантности и доверительных границ по ГОСТ Р 50779.50-95. Можно, например, поступить следующим образом. Приравняем одну из толерантных границ (любую) соответствующему предельному значению признака качества (например, xв = b при 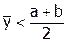 или xн = а при
или xн = а при  ). Математически это означает, что фиксированная таким образом толерантная граница определена с доверительной вероятностью равной 1. Остается найти другую толерантную границу с уровнем доверия:
). Математически это означает, что фиксированная таким образом толерантная граница определена с доверительной вероятностью равной 1. Остается найти другую толерантную границу с уровнем доверия:
g = 2 - b -1 = 1 - b,
поскольку в соответствии с (6.19) требуется, чтобы для суммы уровней доверия обеих
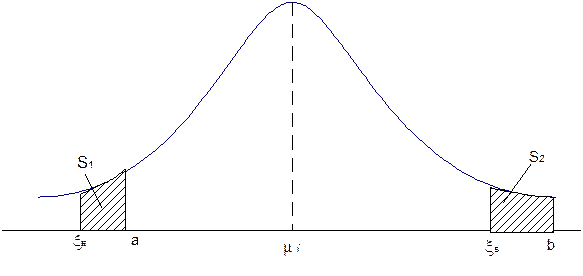
Рисунок 6.2
толерантных границ выполнялось соотношение g1+ g2 = 2 ‑ b. Например, для случая 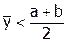 зафиксируем xв = b, тогда из (6.19) можно получить:
зафиксируем xв = b, тогда из (6.19) можно получить:

или 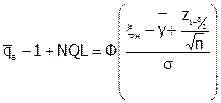 ,
,
где обозначено 
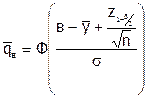 - доля изделий с признаками качества yi < в, вполне определяемая по выборочному среднему значению и исходным данным плана контроля. Окончательно для этого случая нижнюю толерантную границу можно рассчитать по формуле:
- доля изделий с признаками качества yi < в, вполне определяемая по выборочному среднему значению и исходным данным плана контроля. Окончательно для этого случая нижнюю толерантную границу можно рассчитать по формуле:
 .
.
Решение о соответствии в этом случае принимается, если окажется, что xн ³ а, в противном случае следует принять решение о несоответствии партии.
Аналогично для случая 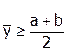 можно получить:
можно получить:
xн = а;
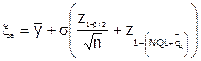 ,
,
где  - доля изделий с признаками качества y < а.
- доля изделий с признаками качества y < а.
Правило принятия решения в этом случае основывается на сравнении xв с b: если xв ≤ b, то партия соответствует требованиям, предъявляемым к уровню её несоответствий; если xв > b, то партия не соответствует требованиям.
Если подходить с чисто практической точки зрения, то, очевидно, что расчет по формулам метода толерантных границ значительно сложнее, чем расчет по методу доверительных границ. Сложность определения толерантных границ существенно возрастает в случае неизвестной дисперсии, и тем более при распределении признака качества, отличном от нормального закона. И вообще, трудно найти причины, по которым исполнитель (разработчик плана выборочного контроля) предпочтёт метод толерантных границ более простому методу доверительных границ. Однако, математический подход к определению толерантных границ существенным образом может помочь технологам и конструкторам при установке и корректировке допусков на количественные признаки качества.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1001; Нарушение авторских прав?; Мы поможем в написании вашей работы!