Временные характеристики звеньев объектов систем

Для того, чтобы можно было сравнивать поведение объектов и систем во времени, используют временные характеристики или реакции на некоторые типовые воздействия, полученные при одинаковых условиях.

Переходной процесс h(t)– это реакция объекта или системы на единичное входное воздействие, полученная при нулевых условиях.

Импульсный переходной процесс – реакция объекта или системы на воздействие в виде δ-функции, полученная при нулевых начальных условиях.

Единичная ступенчатая функция и δ-функция относятся к обобщенным функциям, обладающими рядом специфических свойств.

Единичное ступенчатое воздействие:

0, при t<0

1(t)=

1, при t≥0 или

0, при t<0

1(t)= 1/2, при t=0

0, при t>0,

0, при t≠0

δ(t)=

∞, при t=0.

Функция δ(t) описывает импульс, длительность которого стремится к 0, а амплитуда удовлетворяет следующим условиям:

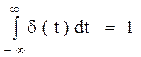
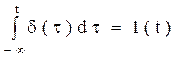
Фильтрующие свойства дельта-функции δ(τ):

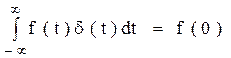
Производная определяется из следующего соотношения:

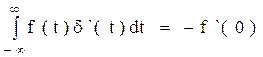
Соответственно:

Преобразование Лапласа:

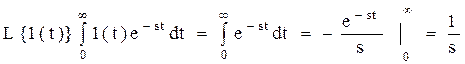
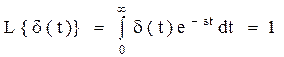
Как известно линейные системы удовлетворяют принципу суперпозиции т.е. реакция системы но воздействие, состоящее из суммы нескольких воздействий равна сумме реакций на каждое воздействие отдельно взятое (при одних и тех же начальных условиях). Это позволяет разбивать системы на элементы с одним входом и упрощать их анализ.

Функции, описывающий переходный процесс и импульсный переходный процесс называются переходной и весовой функциями. Обозначаются обычно h(t) и w(t).

В преобразованиях Лапласа:

H(s)=W(s)/s – (изображение по Лапласу единичной ступенчатой функции )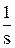

H(s)=W(s)/s=L{h(t)}

L{ω(t)}=W(s)1=W(S)

т.е. изображение по Лапласу весовой функции есть передаточная функция в изображениях по Лапласу. Поскольку деление на s изображения функции соответствует интегрированию оригинала, то переходная функция

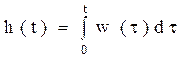
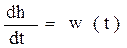
т.е. весовая функция – производная от переходной функции.

Можно использовать интегральную форму уравнения динамики, полученную из следующих преобразований:

Y(s)=W(s)X(s)

X- вход в преобразованиях Лапласа;

Y- выход;

W – передаточная функция.

y(t)=L^-1{W(s)X(s)}=

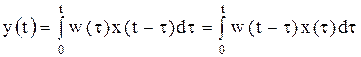
Интеграл свертки

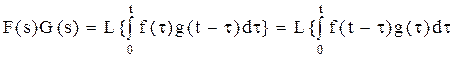
По свойству преобразований Лапласа произведение изображений, получается преобразованием интеграла свертки оригиналов.

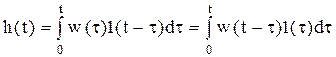-интегральная

форма записи переходного процесса

Аналогично

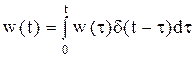- интегральная форма записи весовой функции.

Дата добавления: 2014-01-15