Частотные характеристики линейных объектов

Комплексной частотной характеристикой называется весовая функция объекта или системы в преобразованиях Фурье, т.е.

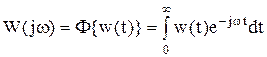
Зачастую комплексная частотная характеристика (КЧХ) получается путем замены в передаточной функции комплексного аргумента s=σ+jω на jω, что соответствует принятию σ=0. Это позволяет получать частотную характеристику для расходящихся весовых функций, для которых преобразование Фурье не существует.

Комплексная частотная характеристика является комплексной функцией действительного аргумента – круговой частоты ω, единица измерения которой – рад/с

ω=2πf.

КЧХ может бать представлена в виде

W(jω)=ReW(jω)+jImW(jω) или W(jω)=A(ω)e^jφ(ω)

A(ω)-модуль вектора;

φ(ω)-фаза вектора или

амплитудная характеристика A(ω) АЧХ

и

φ(ω)-фазовая частотная характеристика ФЧХ.

т.е. A(ω)=|W(jω)|=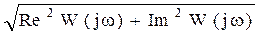

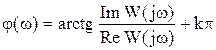
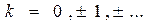
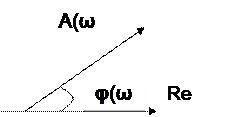Im

Физический смысл АЧХ и ФЧХ: если на вход линейной системы подать гармонический сигнал, то на выходе после окончания переходных процессов также будет гармонический сигнал, той же частоты что и на входе. Отношения амплитуд гармонических сигналов на выходе к амплитуде входного сигнала в зависимости от частоты входного сигнала в установившемся режиме и есть АЧХ.

ФЧХ- это зависимость смещения фазы выходного гармонического сигнала относительно входного от частоты входного сигнала.

Достаточно часто также используется логарифмические частотные характеристики: ЛАХ (логарифмическая амплитудная характеристика) и ЛФХ (логарифмическая фазовая характеристика)

L(θ)=20lgA(θ)

θ=lg(ω)

ψ(θ)=γ(θ)

При построении амплитудной логарифмической характеристики по оси ординат откладывается логарифм амплитудной характеристики, умноженный на 20, причем изменения амплитуды в 10 раз соответствует изменению ЛАХ на 20 децибел (дБ).

Изменение частоты ω в 10 раз соответствует изменению θ на 1 декаду.

По оси абсцисс откладывается аргумент в декадах.

Использование логарифмических характеристик зачастую упрощает анализ и синтез систем и делает более наглядным графические изображения характеристик.

Дата добавления: 2014-01-15