Системы счисления. Системой счисления называют систему приемов и правил, позволяющих устанавливать взаимно однозначное соответствие между любым числом и его представлением в

Системой счисления называют систему приемов и правил, позволяющих устанавливать взаимно однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов.

Можно сказать, что система счисления – это способ записи чисел с помощью заданного набора специальных символов (цифр) и сопоставления этим записям реальных значений.

Все системы счисления можно разделить на непозиционные и позиционные.

Непозиционные системы счисления появились значительно раньше позиционных.

В непозиционных системах счисления значение каждого символа не зависит от того места (позиции), на котором он стоит.

Примером такой системы счисления является римская, в которой для записи чисел используются буквы латинского алфавита. При этом буква I всегда означает единицу, буква V —пять, X — десять, L — пятьдесят, C — сто, D — пятьсот, M — тысячу и т.д. Например, число 264 записывается в виде CCLXIV. Недостатком непозиционных систем счисления является отсутствие формальных правил записи чисел и, соответственно, огромная сложность арифметических действий с многозначными числами.

Правила выполнения вычислений с многозначными числами в позиционной системе счисления были разработаны средневековым математиком Мухамедом аль-Хорезми и в Европе были названы алгоритмами (от латинского написания имени аль-Хорезми – Algorithmi).

Позднее были изобретены позиционные системы счисления, которыми мы пользуемся по сей день, так как выполнение вычислений в таких системах во много раз проще, чем в непозиционных.

Позиционная система счисления – способ записи чисел, при котором используется ограниченное количество знаков, и значение каждого знака зависит от места (позиции), которое он занимает в числе.

Примером позиционной системы счисления является привычная нам десятичная система. Так, в десятичной записи числа 3 931 используются два знака (цифры) «3», но при этом одна из них означает «три тысячи», а вторая – «тридцать».

Мы настолько привыкли к такой записи чисел, что даже не задумываемся, почему так происходит. Разберемся в этом более подробно.

Дело в том, в позиционных системах счисления запись любого целого числа можно представить в виде

где A – число,

a_i – i-й разряд числа,

m – номер разряда (позиции в числе).

Вычислить значение числа можно, руководствуясь правилом:

,

где N – основание системы счисления.

Основание позиционной системы счисления определяет ее название. В двоичной системе счисления используются только две цифры: 0 и 1. В восьмеричной системе счисления для записи чисел используется восемь цифр (0,1,2,3,4,5,6,7). Если основание больше 10 и общепринятых цифр не хватает, используют другие символы – обычно буквы латинского алфавита. Например, в шестнадцатеричной системе счисления для записи чисел используются цифры от 0 до 9 и заглавные латинские буквы A, B, C, D, E, F.

В нашем примере используется десятичная система счисления, т.е. основание системы счисления равно 10, поэтому:

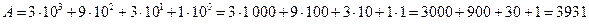
Для того, чтобы пояснить, в какой системе счисления записано число, указывают основание системы счисления в качестве нижнего индекса, например:

3931₁₀ – число в десятичной системе счисления,

111101011011₂ – это же чисто в двоичной системе счисления.

Для рассмотрения правил перевода числа из одной системы счисления в другую используется уже знакомая нам запись числа в виде суммы

.

При этом a_i – цифры числа в исходной системе счисления, N – основание исходной системы счисления. Арифметические операции выполняются по правилам новой системы счисления, и результат также записывается знаками новой системы.

Обратное преобразование выполняется следующим образом: исходное число делится на основание новой системы счисления по правилам исходной системы счисления, при этом отдельно записывается частное и остаток от деления.

Деление продолжается до тех пор, пока частное не будет равно 0. Результат получается путем последовательной записи остатков от деления в обратном порядке.

Так как в основу вычислительных систем положена двоичная система счисления, ограничимся ее рассмотрением. Например, требуется перевести число 1101₂ в десятичную систему:

Переведем число 13₁₀ в двоичную систему:

13:2=6, остаток 1

6:2=3, остаток 0

3:2=1, остаток 1

1:2-0, остаток 1.

Результат: 1101₂.

Арифметические операции, выполняемые в позиционных системах счисления, выполняются по следующим правилам:

· операция сложения выполняется поразрядно, начиная с младших разрядов в слагаемых;

· в каждом одноименном разряде слагаемых суммируются соответствующие цифры и перенос из предыдущего разряда суммы;

· если сумма цифр одноименных разрядов слагаемых и переноса меньше основания системы счисления, то перенос в следующий разряд равен нулю, если равна или больше — то равен единице.

Мы хорошо знакомы с арифметическими действиями над десятичными числами – это так называемые вычисления «в столбик».

Для осуществления арифметических операций над двоичными числами необходимо знать несложные таблицы сложения и умножения двоичных цифр:

Сложение (z=x+y)		Умножение (z=x*y)
x	y	z		x	y	z

Подробнее арифметические операции над двоичными числами будут рассмотрены на практическом занятии.

Дата добавления: 2014-01-15