
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Відношення між множинами. Геометричне зображення множин
|
|
|
|
В множині можуть бути виділені підмножини.
Означення. Множина  називається підмножиною множини
називається підмножиною множини  , якщо кожен елемент множини
, якщо кожен елемент множини  належить множині
належить множині  .
.
Це позначається як  (
(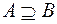 ) – «
) – « включається в
включається в  » (
» ( включає
включає  ), де
), де  – знак нестрогого включення.
– знак нестрогого включення.
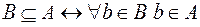 .
.
Наприклад: 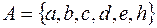 ,
, 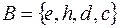 ,
,  –
–  – підмножина
– підмножина  .
.
Зауваження. Слід підкреслити відмінність між відношенням належності 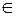 і відношенням включення
і відношенням включення  . Як вже зазначалося, множина
. Як вже зазначалося, множина  може бути своєю підмножиною
може бути своєю підмножиною 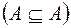 , але не може входити до складу своїх елементів (
, але не може входити до складу своїх елементів (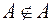 ). Навіть у разі одноелементної множини розрізняють саму множину
). Навіть у разі одноелементної множини розрізняють саму множину  та її єдиний елемент
та її єдиний елемент 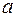 .
.
Означення. Множини  і
і  називаються рівними, якщо вони складаються з одних і тих самих елементів, тобто
називаються рівними, якщо вони складаються з одних і тих самих елементів, тобто 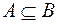 і
і  .
.
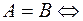
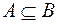 і
і  .
.
Приклад. 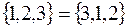 ,
, 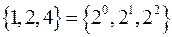 .
.
Якщо  и
и 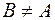 , то
, то  називається власною, строгою чи істинною підмножиною
називається власною, строгою чи істинною підмножиною  . Позначення:
. Позначення: 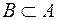 , де
, де  – знак строгого включення.
– знак строгого включення.
Очевидно, що для будь-якої множини 
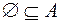 і
і 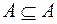 .
.
 і
і  називаються невласними підмножинами множини
називаються невласними підмножинами множини  .
.
Для кожної множини  існує множина, елементами якої є всі її підмножини.
існує множина, елементами якої є всі її підмножини.
Означення. Множина, елементами якої є всі підмножини множини  і тільки вони, називається булеаном (або множиною підмножин) множини
і тільки вони, називається булеаном (або множиною підмножин) множини  і позначається
і позначається 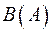 . Відносно елементів булеана множина
. Відносно елементів булеана множина  є універсумом. (Тобто, універсальна множина – це множина, підмножинами якої є всі множини, що розглядаються,)
є універсумом. (Тобто, універсальна множина – це множина, підмножинами якої є всі множини, що розглядаються,)
У разі скінченної підмножини  , що складається з
, що складається з 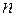 елементів, булеан
елементів, булеан 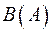 містить
містить 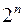 елементів:
елементів:
 .
.
Легко побачити, що число елементів булеана 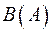 залежить від числа елементів универсуму
залежить від числа елементів универсуму 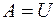 . Наприклад, якщо
. Наприклад, якщо 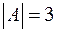 , то маємо
, то маємо 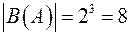 .
.
Приклад. Розглянемо утворення булеана множини:
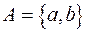 :
:
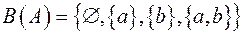 ;
;
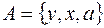 :
:
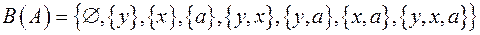 .
.
Перша й остання підмножини невласні, інші – власні.
Порожня множина має властивість:
має властивість: 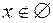 при будь-якому
при будь-якому  . Універсальна множина
. Універсальна множина 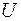 має властивість:
має властивість: 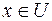 при будь-якому
при будь-якому  .Множини і відношення між ними зручно задавати графічно за допомогою так званих діаграм Ейлера-Венна. Діаграми Ейлера-Венна (Джон Венн (1834-1923) англійський логік і математик, професор Кембриджського університету) є геометричним зображенням множин. Множина зображується замкненою кривою довільної форми (найчастіше – кругом). Точки, які лежать всередині замкненої кривої, можна розглядати як елементи відповідної множини.
.Множини і відношення між ними зручно задавати графічно за допомогою так званих діаграм Ейлера-Венна. Діаграми Ейлера-Венна (Джон Венн (1834-1923) англійський логік і математик, професор Кембриджського університету) є геометричним зображенням множин. Множина зображується замкненою кривою довільної форми (найчастіше – кругом). Точки, які лежать всередині замкненої кривої, можна розглядати як елементи відповідної множини. Наприклад:
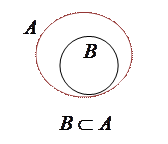
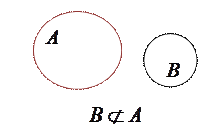
Універсум 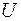 на діаграмах Ейлера-Венна зображується у вигляді прямокутника.
на діаграмах Ейлера-Венна зображується у вигляді прямокутника.

Діаграму Ейлера-Венна можна розглядати як окремий випадок задання множини переліком його елементів. В цьому випадку всередині діаграми Ейлера-Венна можуть бути зображені символічні позначення елементів.
Наприклад: На наступній діаграмі Ейлера-Венна задані множини 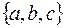 ,
, 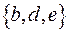 в універсумі
в універсумі 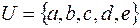 :
:
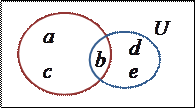
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 6280; Нарушение авторских прав?; Мы поможем в написании вашей работы!