
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЛЕКЦИЯ № 7
|
|
|
|
Механизм с гидроцилиндром. Расчетная схема механизма показана на рис. 2.20, а. На схеме не указаны силы инерции и моменты сил инерции звеньев, которыми можно пренебречь ввиду их малости.
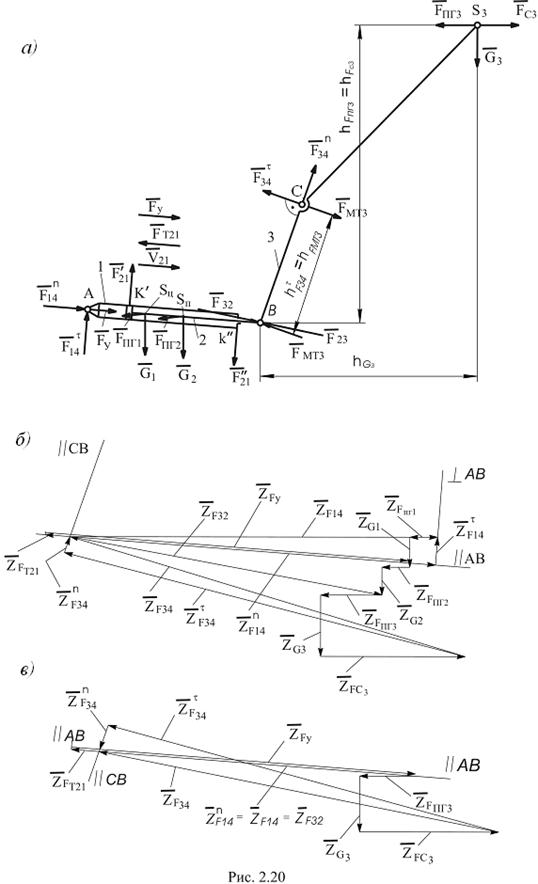
На первом этапе расчета определим силы в кинематических парах А, В, С рассматривая весь механизм как неделимую структурную единицу. При этом мысленно “заморозим” поршень в гидроцилиндре в расчётном положении.
Для системы сил, приложенных к звену 3, составим уравнение моментов относительно точки В
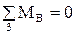 .
.
или
 .
.
Здесь через  с индексом обозначены плечи соответствующих сил относительно точки
с индексом обозначены плечи соответствующих сил относительно точки 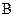 механизма. Плечи сил могут быть определены непосредственно по схеме механизма, изображенного в масштабе (рис. 2.20, а).
механизма. Плечи сил могут быть определены непосредственно по схеме механизма, изображенного в масштабе (рис. 2.20, а).
С этой целью момент трения 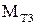 представлен парой сил
представлен парой сил  , приложенных в точках С и В,
, приложенных в точках С и В,
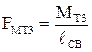 .
.
Неизвестная касательная составляющая силы 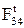 определяется как
определяется как
 . (2.111)
. (2.111)
Для системы сил, приложенных к звеньям 1 и 2 гидроцилиндра, составим уравнение равновесия в виде суммы моментов сил относительно точки 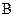
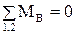 .
.
 .
.
Здесь плечи сил на звеньях 1,2 определяются аналогично плечам на звене 3.
Значение и направление силы 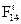 определяется из соотношения:
определяется из соотношения:
 . (2.112)
. (2.112)
Для определения нормальных составляющих сил в кинематических парах составим векторное уравнение равновесия механизма с “замороженным” гидроцилиндром, сгруппировав силы по звеньям:
 . (2.113)
. (2.113)

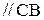
Здесь силы, известные по величине и направлению подчеркнуты двумя чертами, неизвестные по величине нормальные составляющие сил подчеркнуты одной чертой.
Решим векторное уравнение (2.113) графически – путем построения плана сил (рис. 2.20, б). Масштабный коэффициент сил определим по максимальной известной силе, у нас 
 . (2.114)
. (2.114)
Величина масштабного коэффициента определяет отрезки, изображающие другие известные силы
 и т.д.
и т.д.
Построение силового многоугольника. Проведем линию действия силы  параллельно
параллельно 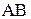 . Из произвольной точки на этой линии, являющейся точкой конца вектора силы
. Из произвольной точки на этой линии, являющейся точкой конца вектора силы  , откладываем отрезок
, откладываем отрезок 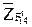 , изображающий вектор силы
, изображающий вектор силы  , и т.д. согласно уравнению сил (2.113). Из конца последнего отрезка известной силы
, и т.д. согласно уравнению сил (2.113). Из конца последнего отрезка известной силы 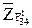 проведем линию действия силы
проведем линию действия силы  параллельно
параллельно 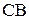 . Точка пересечения двух направлений определяет на них отрезки
. Точка пересечения двух направлений определяет на них отрезки  и
и  , изображающие векторы сил
, изображающие векторы сил  и
и  .
.
 .
.
Полный вектор каждой силы определяется с помощью полученного многоугольника сил и равен геометрической сумме нормальной и касательной составляющих.
Используя построенный многоугольник сил (рис. 2.20, б), можно определить неизвестную силу в шарнире В и уравновешивающую силу 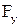 .
.
Для определения силы, действующей в шарнире В, рассмотрим равновесие звена 3
 .
.
Или
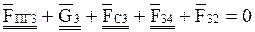 , (2.115)
, (2.115)
откуда 
При определении уравновешивающей силы 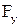 , приложенной к ведущему звену 2, следует учесть силы
, приложенной к ведущему звену 2, следует учесть силы  и
и  , действующие в поступательной кинематической паре звеньев 1 и 2 в точках
, действующие в поступательной кинематической паре звеньев 1 и 2 в точках 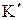 и
и 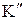 . Направление этих сил известно – перпендикулярно оси цилиндра, а величина их подлежит определению.
. Направление этих сил известно – перпендикулярно оси цилиндра, а величина их подлежит определению.
Запишем уравнение равновесия звена 2
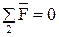 .
.
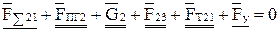 . (2.116)
. (2.116)
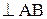

Здесь  ,
,
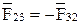 .
.
Величины 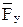 и
и 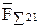 определяются из плана сил (рис. 2.20, б).
определяются из плана сил (рис. 2.20, б).
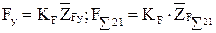 .
.
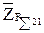 ввиду малости на плане сил не показана.
ввиду малости на плане сил не показана.
Уравновешивающая сила как движущая сила направлена вдоль линии действия гидроцилиндра АВ. Знак уравновешивающей силы положителен, т.к. ее направление совпадает с направлением положительной скорости 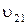 .
.
Силу взаимодействия звеньев 1 и 2 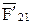 можно определить из уравнения моментов:
можно определить из уравнения моментов:
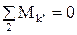 ;
;
 ;
;
откуда
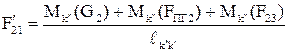 . (2.117)
. (2.117)
Плечи сил определяются по схеме механизма.
Сила  определяется как разность сил
определяется как разность сил  и
и  .
.
В реальных механизмах с гидроцилиндром, как правило, сила тяжести звеньев 1 и 2 гидроцилиндра бывает пренебрежимо мала по сравнению с силой тяжести звена 3 и другими силами, приложенными к выходному звену.
В этом случае силовой расчет механизма значительно упрощается.
Для рассматриваемого механизма с гидроцилиндром при пренебрежении массами звеньев 1 и 2 на звеньях механизма будут действовать силы  .
.
Касательная составляющая силы в шарнире 
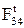 не изменит своего значения, тогда как касательная составляющая силы в шарнире А
не изменит своего значения, тогда как касательная составляющая силы в шарнире А 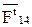 и силы
и силы 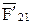 и
и 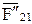 будут равны нулю. Таким образом, сила в шарнире
будут равны нулю. Таким образом, сила в шарнире 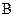
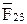 окажется направленной вдоль линии оси гидроцилиндра.
окажется направленной вдоль линии оси гидроцилиндра.
План сил такого механизма представлен на рис. 2.20, в.
2.4.4. Применение принципа возможных перемещений для определения уравновешивающего момента или уравновешивающей силы
Согласно принципу возможных перемещений сумма элементарных работ всех сил и моментов, приложенных к системе, находящейся в равновесии, на возможных перемещениях системы равна нулю
в равновесии, на возможных перемещениях системы равна нулю
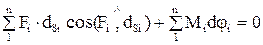 . (2.118)
. (2.118)
Для механизма возможными перемещениями звеньев и точек приложения сил будут их действительные перемещения, являющиеся функциями положения начального звена. Если приложить к звеньям механизма силы инерции, то можно рассматривать его в состоянии динамического равновесия.
Так как силы, действующие в кинематических парах, являются внутренними, то уравнение (2.118) позволяет найти величину уравновешивающего момента или уравновешивающей силы без их предварительного определения.
Записанное выше уравнение (2.118) неудобно для практического использования, поэтому возьмем сумму элементарных работ в единицу времени; тогда, принимая во внимание, что
 и
и 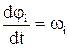 ,
,
получим
 , (2.119)
, (2.119)
где суммирование проводится по всем 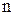 силам и
силам и  моментам сил всех звеньев механизма, а каждое слагаемое представляет собой мощность силы или момента.
моментам сил всех звеньев механизма, а каждое слагаемое представляет собой мощность силы или момента.
Так как скорости точек приложения сил и угловые скорости звеньев известны по величине и направлению из кинематического расчета, то единственным неизвестным является искомая величина уравновешивающего момента (или уравновешивающей силы).
Для кривошипно-ползунного механизма, схема которого представлена на рис. 2.21, уравнение (2.119) запишется
 (2.120)
(2.120)
Углы между направлениями векторов сил и скоростей можно взять из плана механизма (рис. 2.21). На рис. 2.21 показан только один из углов –  . Так как направление приложенного уравновешивающего момента
. Так как направление приложенного уравновешивающего момента 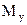 взято на схеме механизма произвольно, то при отрицательном значении
взято на схеме механизма произвольно, то при отрицательном значении 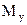 его направление следует изменить на противоположное.
его направление следует изменить на противоположное.

Для механизма с гидроцилиндром, схема которого приведена на рис. 2.22, уравнение (2.119) будет иметь вид
 (2.121)
(2.121)
Углы между направлениями сил и скоростей, а также знак уравновешивающей силы определяется аналогично предыдущему примеру. На рис. 2.22 показан лишь угол между векторами 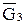 и
и 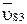
 .
.

Основной смысл применения принципа возможных перемещений заключается в определении уравновешивающего момента или уравновешивающей силы без проведения силового анализа механизма (без определения сил в кинематических парах). Метод используют, как правило, для проверки силового расчета.
2.4.5.Рычаг Жуковского
Графоаналитическое решение уравнения (2.119) предложил Н.Е. Жуковский в виде рычага Жуковского.
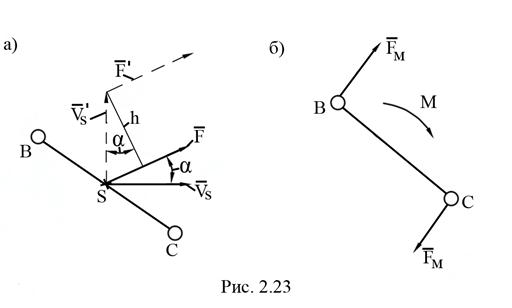
Пусть к звену 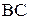 в точке
в точке  (рис. 2.23, а) приложена сила
(рис. 2.23, а) приложена сила  любой природы.
любой природы. 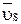 - вектор абсолютной скорости точки приложения силы
- вектор абсолютной скорости точки приложения силы  . Угол
. Угол 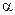 есть угол
есть угол 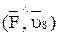 .
.
Повернем вектор скорости 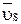 в любую сторону на 90° и в конец повернутого вектора скорости перенесем параллельно самому себе вектор силы
в любую сторону на 90° и в конец повернутого вектора скорости перенесем параллельно самому себе вектор силы  (
( и
и 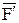 на рис. 2.23, а).
на рис. 2.23, а).
|
Тогда  . Так как
. Так как  и
и 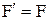 , то
, то
 . (2.122)
. (2.122)
Здесь  - момент силы
- момент силы 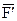 относительно точки
относительно точки  - точки начала вектора абсолютной скорости
- точки начала вектора абсолютной скорости 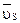 .
.
Если на звено действует момент сил 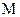 (рис. 2.23, б),то его можно представить парой сил
(рис. 2.23, б),то его можно представить парой сил  , и все сказанное выше относится и к силам
, и все сказанное выше относится и к силам  .
.
Если учесть, что начало векторов абсолютных скоростей всех точек располагается в полюсе плана скоростей механизма, то теорему Жуковского можно сформулировать следующим образом.
Если векторы всех сил, приложенных к различным точкам звеньев механизма, перенести параллельно самим себе в одноименные точки повернутого на 90° плана скоростей, приняв фигуру плана за жесткий рычаг, то момент каждой силы относительно полюса плана скоростей будет пропорционален ее мощности, а сумма моментов всех указанных сил будет равна нулю.
При этом все моменты, в том числе и уравновешивающий момент, должны быть заменены парами сил. Пара сил  , заменяющая уравновешивающий момент, равна
, заменяющая уравновешивающий момент, равна  .
.
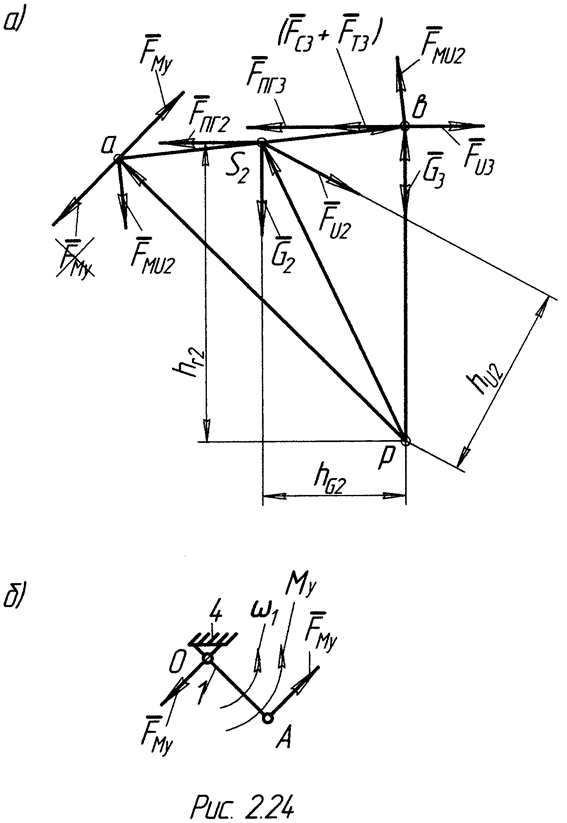
Рычаг Жуковского, построенный для кривошипно-ползунного механизма, изображенного на рис. 2.19, а, представлен на рис. 2.24, а. План скоростей
(рис. 2.9, б) повернут на 90° против часовой стрелки. Сила  произвольно направлена вниз от точки а плана.
произвольно направлена вниз от точки а плана.
Сумма моментов сил относительно полюса р рычага Жуковского имеет вид
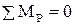 .
.
Или
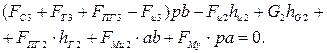 (2.123)
(2.123)
Отсюда
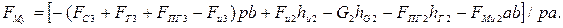 (2.124)
(2.124)
В этом выражении плечи сил определяются из рычага Жуковского путем их замера.
Как видно из формулы, величина силы  не зависит от масштаба построения рычага Жуковского.
не зависит от масштаба построения рычага Жуковского.
Если расчет даст отрицательное значение силы  , то направление силы на рычаге Жуковского следует сменить на противоположное.
, то направление силы на рычаге Жуковского следует сменить на противоположное.
Для определения уравновешивающего момента необходимо полученную силу перенести параллельно самой себе из рычага Жуковского в точку А первичного механизма (рис. 2.24, б), и тогда уравновешивающий момент будет положительным, и иметь вид:
 .
.
Рычаг Жуковского для механизма с гидроцилиндром (рис. 2.20, а) представлен на рис. 2.25. Уравновешивающая сила 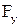 определяется из уравнения
определяется из уравнения
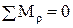 .
.
Или
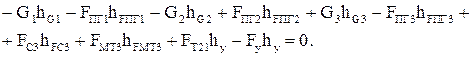 (2.125)
(2.125)
Отсюда
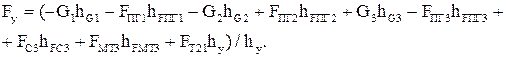 (2.126)
(2.126)

|
Рис. 2.25
Для определения знака уравновешивающей силы необходимо вектор 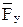 перенести параллельно самому себе из рычага Жуковского на ось гидроцилиндра механизма. Если направление силы
перенести параллельно самому себе из рычага Жуковского на ось гидроцилиндра механизма. Если направление силы 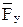 совпадёт с положительным направлением скорости
совпадёт с положительным направлением скорости 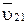 , то и сила
, то и сила 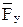 будет также положительной, в противном случае сила
будет также положительной, в противном случае сила 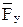 будет отрицательной.
будет отрицательной.
Для механизма, изображенного на рис. 2.20, а, уравновешивающая сила Fy положительна.
Вопросы для самоконтроля.
1. Какова особенность проведения силового анализа механизмов с гидроцилиндром?
2. Как определить знак уравновешивающей силы в гидрорычажных механизмах?
3. Как определяется масштабный коэффициент плана сил?
4. В чём состоит смысл применения принципа возможных перемещений?
5. Как формулируется принцип возможных перемещений?
6. Чему равна мощность силы и момента сил?
7. Как читается теорема Жуковского о жестком рычаге в силовом расчёте?
8. Какое условие является необходимым для использования рычага Жуковского в силовом расчёте?
9. Как определяется уравновешивающая сила или уравновешивающий момент при применении рычага Жуковского?
10. С какой целью определяют уравновешивающую силу или уравновешивающий момент?
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 509; Нарушение авторских прав?; Мы поможем в написании вашей работы!